Nội dung bài viết
© 2025 AI VIET NAM. All rights reserved.
Tác giả: Anh-Khoi Nguyen (AIO2024), Yen-Linh Vu (AIO2024), Dinh-Thang Duong (TA), Phuc-Thinh Nguyen (AIO2024, CM)
Keywords: giải thuật di truyền, genetic algorithm, học ai online
Ở bài trước, chúng ta đã biết được rằng giải thuật Gradient Descent có thể được sử dụng để tìm ra bộ tham số tối ưu nhằm giải quyết bài toán hồi quy tuyến tính. Theo đó, chúng ta cũng đã thảo luận rằng, có rất nhiều giải thuật tối ưu hóa có thể được ứng dụng vào để tìm ra lời giải tối ưu cho bài toán Linear Regression này.
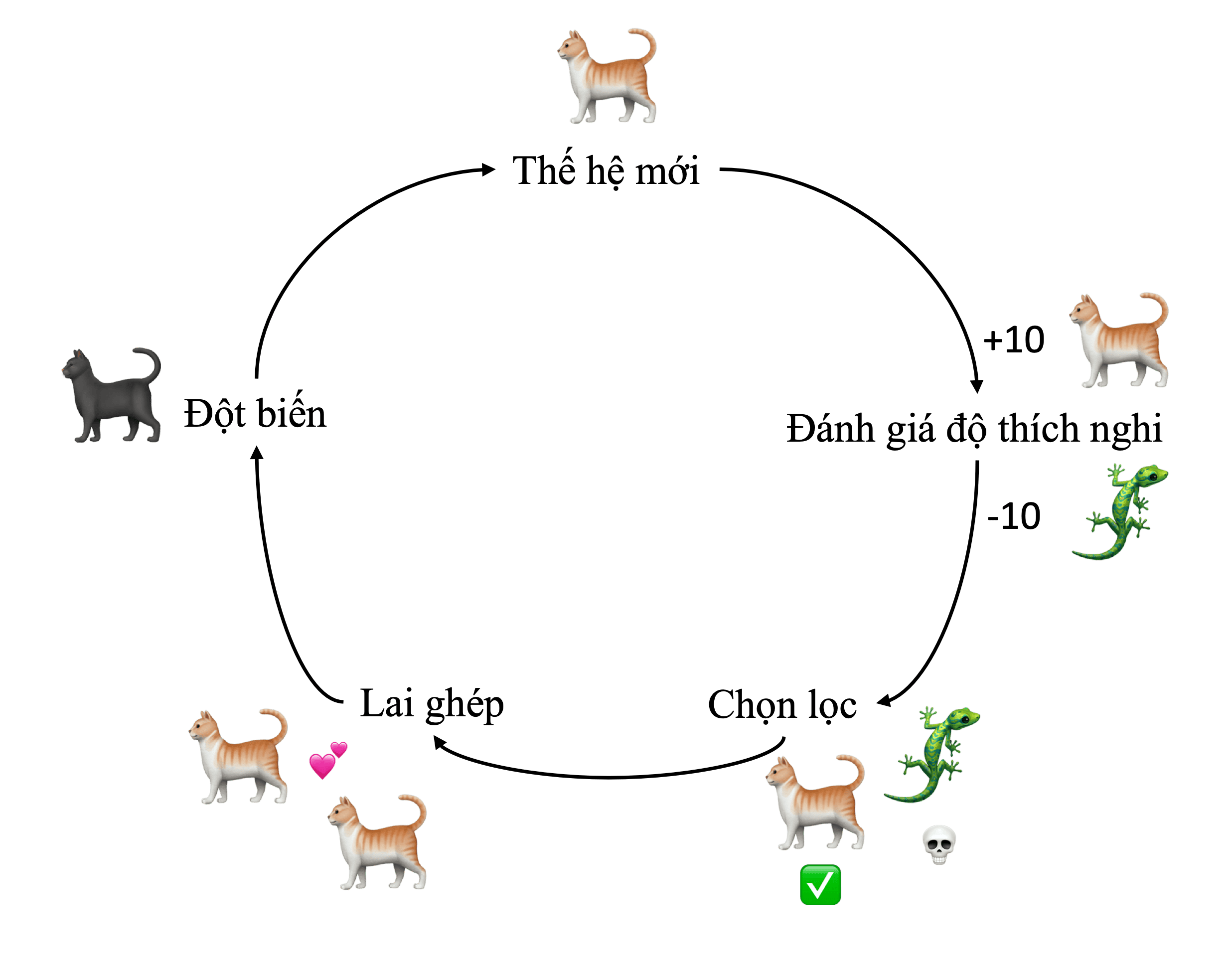 Hình 1: Minh họa về các quá trình diễn ra trong một thế hệ của một quần thể.
Hình 1: Minh họa về các quá trình diễn ra trong một thế hệ của một quần thể.
Song, trên thực tế, không phải lúc nào chúng ta cũng có thể biết rõ hàm số, hay tổng quát là vấn đề cần tối ưu là gì. Đôi khi, chúng ta chỉ biết được hành vi của hàm đó thông qua việc quan sát giá trị đầu vào (input) và giá trị đầu ra (output).
 Hình 2: Minh họa về vấn đề mà ở đó ta chỉ có thể quan sát được giá trị đầu vào và đầu ra.
Hình 2: Minh họa về vấn đề mà ở đó ta chỉ có thể quan sát được giá trị đầu vào và đầu ra.
Khi không biết trước hàm cần giải quyết, đối với một số bài toán như đã đề cập ở đầu bài, việc tối ưu có vẻ như sẽ gặp ít nhiều khó khăn hơn. Vậy câu hỏi đặt ra là, liệu có một giải thuật nào có thể giúp chúng ta tìm ra một kết quả tối ưu kể cả khi không biết hàm số cụ thể của bài toán là gì? Theo đó, chúng ta có thể ứng dụng giải thuật di truyền (Genetic Algorithm) để giải dạng vấn đề này. Để tiếp cận đến giải thuật di truyền một cách dễ dàng nhất, có lẽ chúng ta có thể nghĩ về quá trình mà một quần thể loài vật phát triển qua từng thế hệ trong tự nhiên.
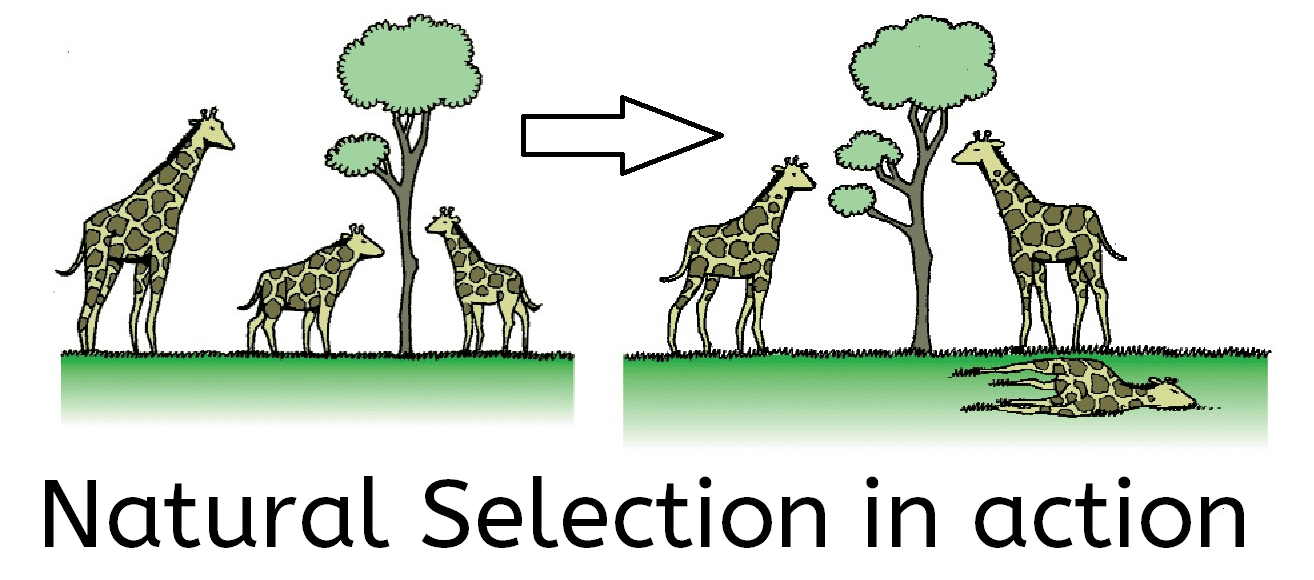 Hình 3: Minh họa về quá trình chọn lọc tự nhiên giữa loài hươu cao cổ. Nguồn: Link.
Hình 3: Minh họa về quá trình chọn lọc tự nhiên giữa loài hươu cao cổ. Nguồn: Link.
Hiểu một cách ngắn gọn rằng, trong một quần thể loài vật, theo thời gian, các cá thể luôn cần phải có sự tiến hóa liên tục qua từng thế hệ để có thể thích nghi và sinh tồn. Các bạn có thể hình dung trong ví dụ ở Hình 3, các con hưu cao cổ với chiều cao hạn chế dần sẽ bị đào thải vì một lẽ hiển nhiên rằng chúng luôn gặp khó khăn khi kiếm thức ăn hằng ngày. Và rằng các cá thể có chiều cao vượt trội sẽ dễ dàng sinh tồn hơn rất nhiều. Chính bởi lẽ đó, toàn bộ các cá thể trong quần thể, đặc biệt là các cá thể mới được sinh ra, cần phải liên tục thích nghi và cải thiện bản thân để có thể tồn tại được trong môi trường.
Để minh họa cho thuật toán di truyền, chúng ta sẽ sử dụng bài toán One-Max. Đây là một bài toán tối ưu đơn giản, trong đó mỗi cá thể là một chuỗi nhị phân gồm các giá trị 0 và 1. Mục tiêu của bài toán là tìm ra chuỗi nhị phân có số lượng ’1’ lớn nhất. Nói cách khác, bài toán yêu cầu tối đa hóa số lượng các bit ’1’ trong một chuỗi. Các cá thể trong quần thể sẽ cạnh tranh với nhau dựa trên số lượng ’1’ trong chuỗi của mình, và thông qua quá trình chọn lọc, đột biến, và lai ghép, các cá thể sẽ tiến hóa để đạt đến lời giải tối ưu.
Bài toán One-Max giúp chúng ta dễ dàng hình dung cách thức hoạt động của thuật toán di truyền, từ khởi tạo quần thể, đánh giá độ phù hợp của từng cá thể, đến các phép toán di truyền như chọn lọc, lai ghép và đột biến.
Trong bài đọc này, chúng mình sẽ cùng nhau thảo luận một thuật toán cơ bản trong giải thuật di truyền dùng để tìm lời giải tối ưu cho một vấn đề. Theo đó, pipeline tổng quan của giải thuật di truyền cơ bản sẽ có dạng như hình sau:
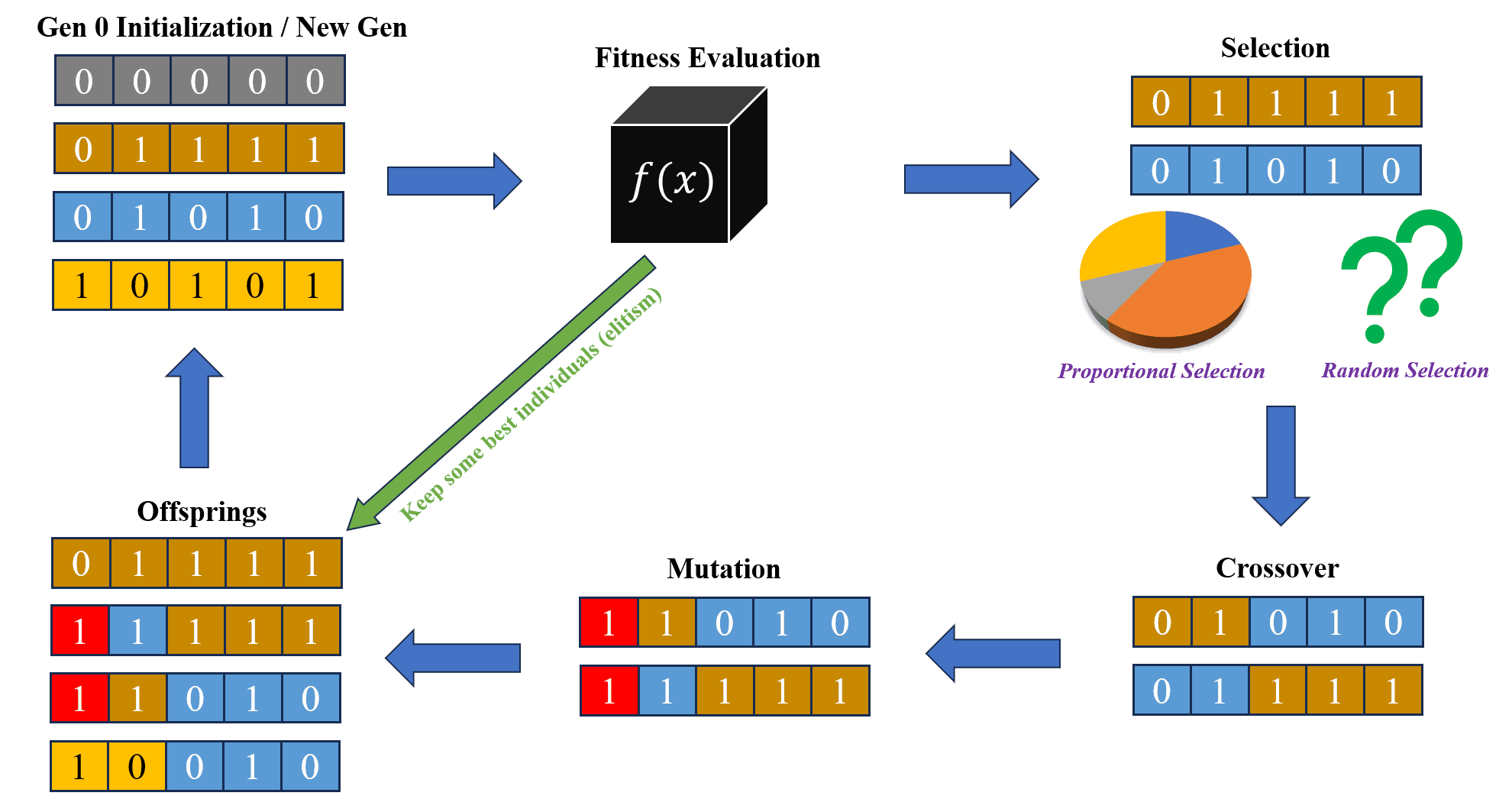 Hình 4: Pipeline cơ bản của giải thuật di truyền.
Hình 4: Pipeline cơ bản của giải thuật di truyền.
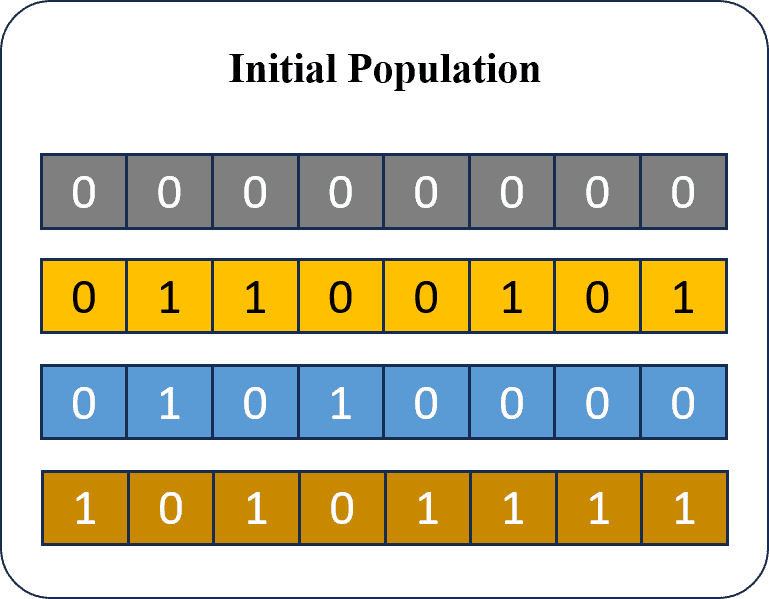 Hình 5: Khởi tạo thế hệ đầu tiên - Gen 0.
Hình 5: Khởi tạo thế hệ đầu tiên - Gen 0.
Như thuật toán khác, trước tiên, chúng ta cần khởi tạo một Quần thể (Population) cho thế hệ đầu tiên, như Hình 5. Theo hình minh hoạ, giả sử chúng ta tạo trước 4 bộ gen, mỗi bộ gen là một hàng, mỗi ô trong bộ gen có thể hiểu là các đặc trưng của gen đó và có giá trị nhị phân (chỉ có thể là 0 hoặc 1).
Kế tiếp, để biết được bộ gen nào có thể thích nghi tốt với môi trường, ta cần một hàm để đánh giá cho khả năng này, gọi là Fitness Evaluation. Một cách tự nhiên mà nói, việc xác định công thức cho hàm đánh giá này là rất khó, chúng ta cần xem xét cụ thể môi trương xung quanh và các yếu tố cần quan tâm của các bộ gen. Hãy lấy ví dụ đơn giản về môi trường sống tự nhiên của động vật như hình bên dưới:
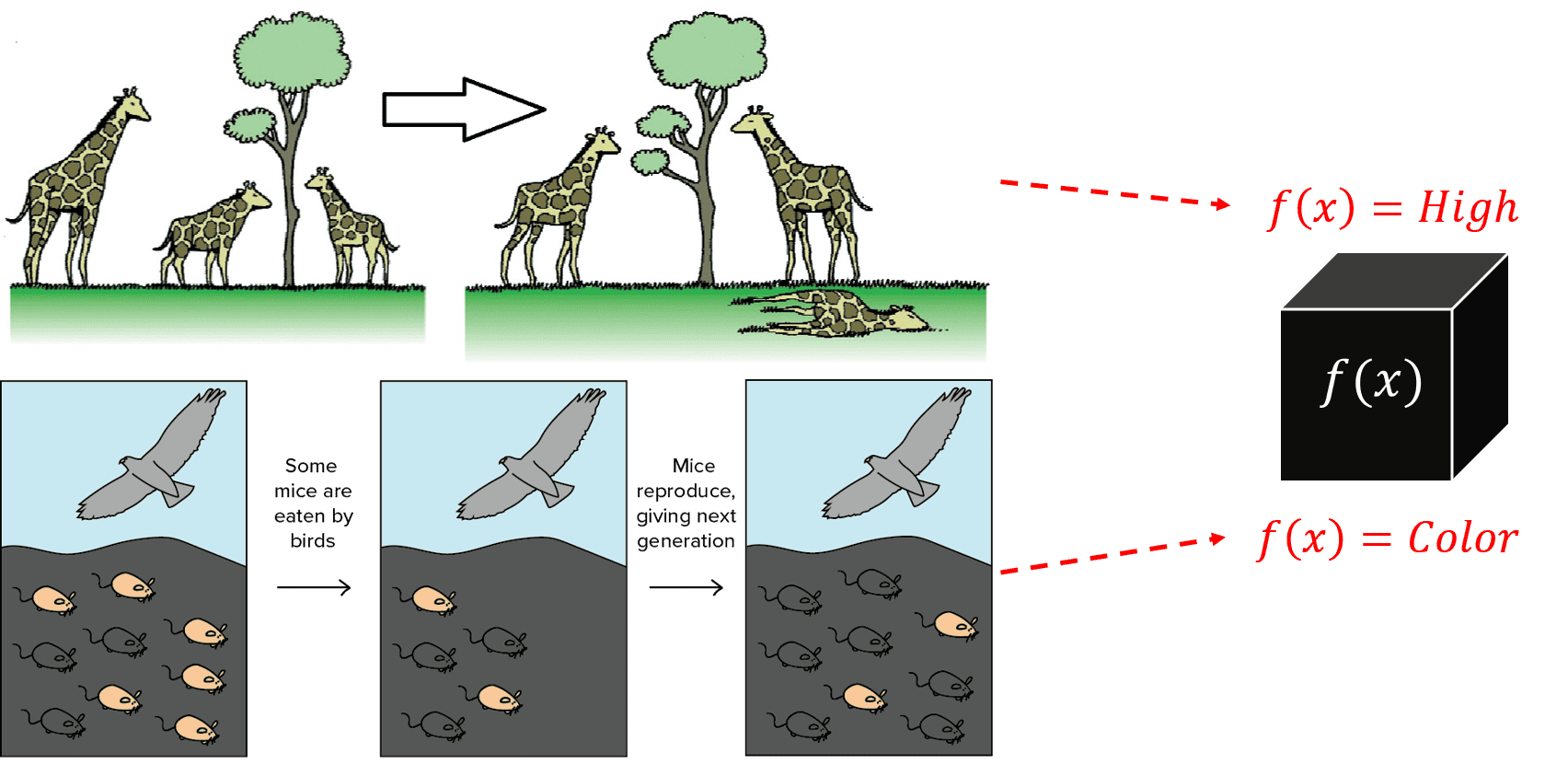 Hình 6: Chọn lọc tự nhiên - Nguồn: Link1 và Link2.
Hình 6: Chọn lọc tự nhiên - Nguồn: Link1 và Link2.
Quan sát Hình 6, với loài hươu cao cổ, sự chọn lọc tự nhiên dựa vào chiều cao của chúng, các con hươu cao cổ có chiều cao “khiêm tốn” sẽ không thể ăn được lá cây, và dần bị đào thải đi. Tuy nhiên, đối với loài chuột, màu sắc mới quyết định thích nghi với môi trường của chúng. Những con chuột có màu sáng hoặc nổi bật sẽ dễ bị phát hiện bởi các loài chim ăn chuột, do đó, các thế hệ chuột sau dần dần chuyển sang màu tối hơn, phù hợp với điều kiện sống của chúng. Chính vì thế, có thể nói:
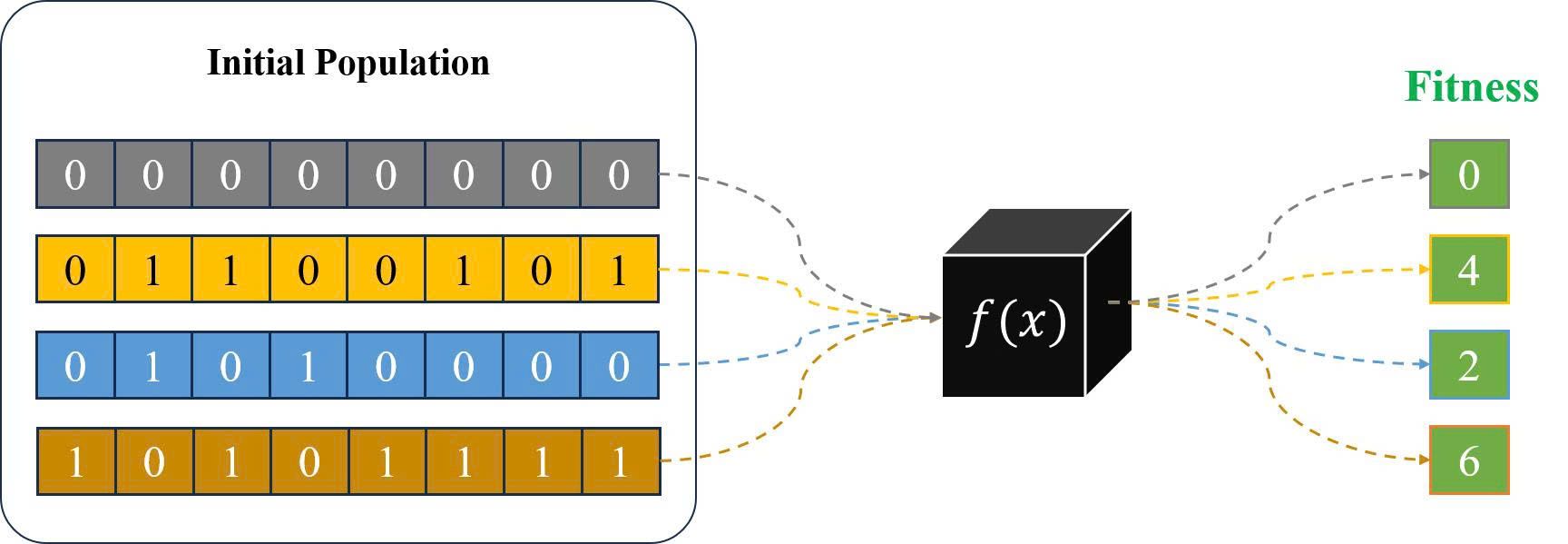 Hình 7: Minh hoạ về Fitness Evaluate.
Hình 7: Minh hoạ về Fitness Evaluate.
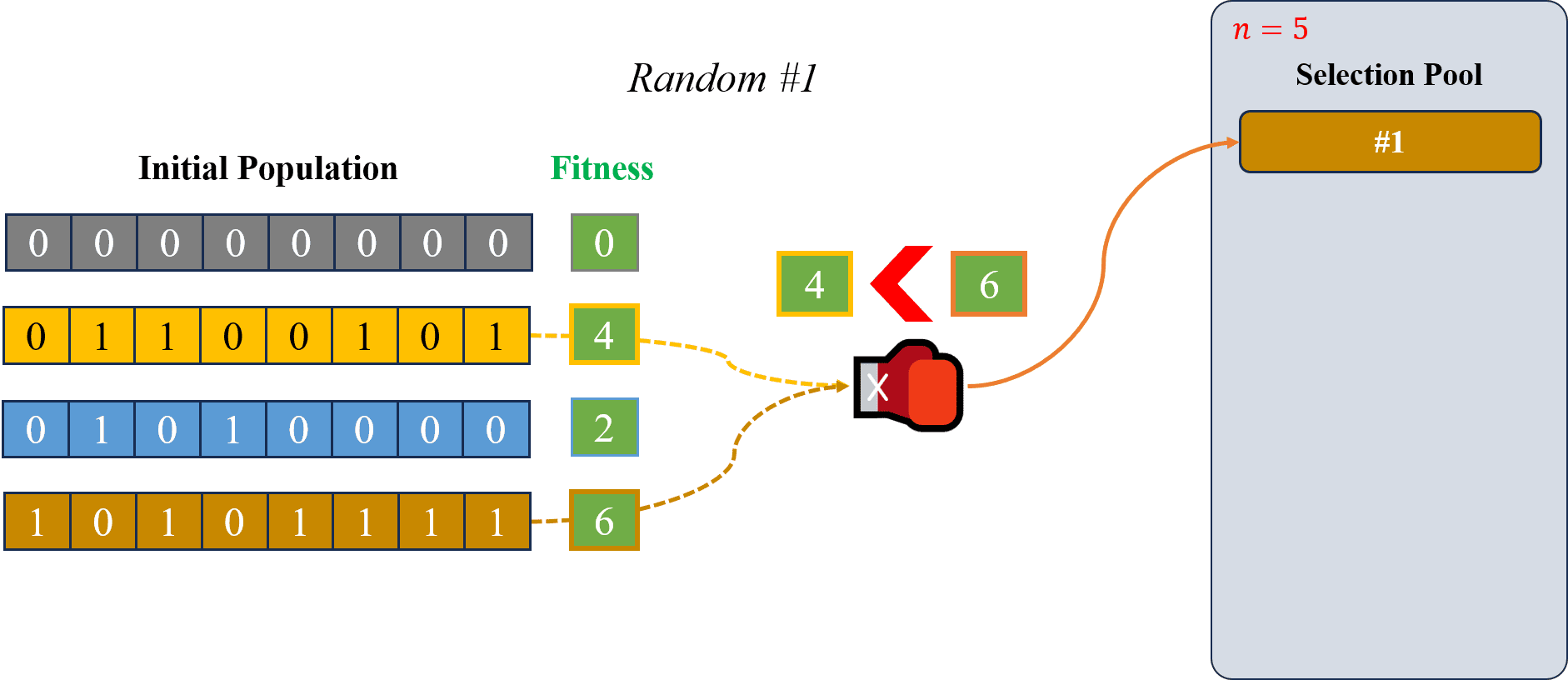 Hình 8: Quá trình chọn lựa cá thể ngẫu nhiên lần thứ nhất.
Hình 8: Quá trình chọn lựa cá thể ngẫu nhiên lần thứ nhất.
Sau khi có được các giá trị Fitness từ bước trên, chúng ta sẽ chọn lựa chọn từng cặp cá thể một cách ngẫu nhiên và xem xét giá trị Fitness của chúng. Cá thể nào có giá trị Fitness lớn hơn (thích nghi tốt hơn) sẽ là cá thể tinh anh và được tham gia vào quá trình lai tạo và đột biến ở các bước tới. Theo như hình minh hoạ ở Hình 8, ta ngẫu nhiên chọn được cặp cá thể màu vàng và màu cam, sau đó, so sánh giá trị Fitness của chúng và kết quả cho thấy cá thể màu cam tốt hơn cá thể màu vàng (). Do đó, ta sẽ chọn cá thể màu cam là cá thể tinh anh và đặt vào trong Selection Pool.
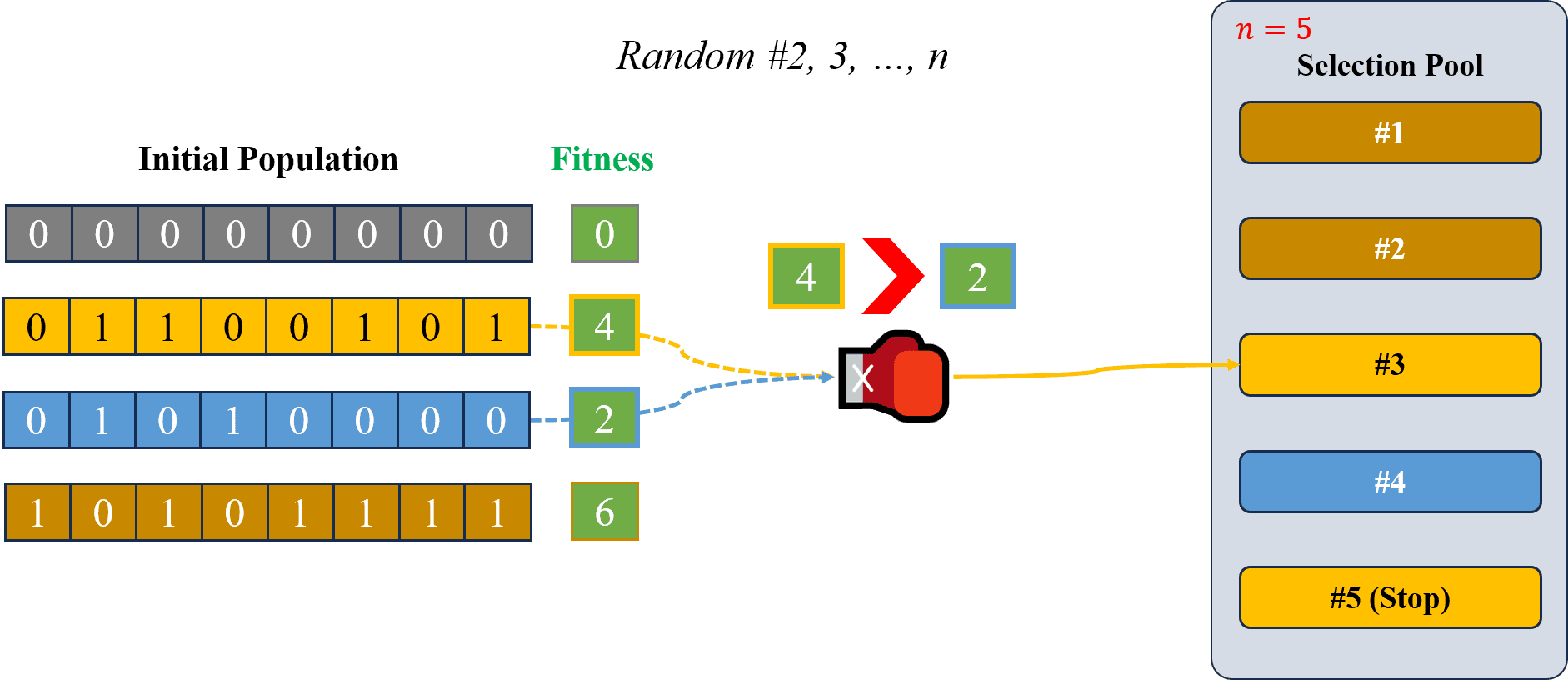 Hình 9: Lặp lại quá trình chọn lựa cá thể ngẫu nhiên.
Hình 9: Lặp lại quá trình chọn lựa cá thể ngẫu nhiên.
Quá trình Selection được lặp lại cho tới khi có đủ số lượng cá thể tinh anh trong Selection Pool như mong muốn thì sẽ tiến hành bước tiếp theo. Như trong Hình 9, ở lần ngẫu nhiên thứ 2 ta được cá thể tinh anh màu cam, tiếp tục lần thứ 3, ngẫu được chọn cặp cá thể vàng và xanh biển, ta được cá thể tinh anh màu vàng, và cứ tiếp tục như thế cho đến khi đủ số lượng cá thể tinh anh () thì dừng lại và chuyển sang bước tiếp theo.
Tại bước này, chúng ta sẽ tiến hành lai tạo các cặp cá thể với nhau để cho ra các cá thể con mới có thể kế thừa các đặc tính tốt từ cha mẹ. Crossover mô phỏng quá trình trao đổi chéo của các nhiễm sắc thể, được minh hoạ như hình bên dưới:
 Hình 10: Minh hoạ quá trình trao đổi chéo của nhiễm sắc thể.
Hình 10: Minh hoạ quá trình trao đổi chéo của nhiễm sắc thể.
Chúng ta sẽ áp dụng cơ chế trao đổi chéo này trong bước này, nhưng không chỉ dừng lại ở trao đổi chéo tại 1 điểm, ta hoàn toàn có thể tăng số lượng điểm trao đổi lên nhiều hơn, như hình minh hoạ sau:
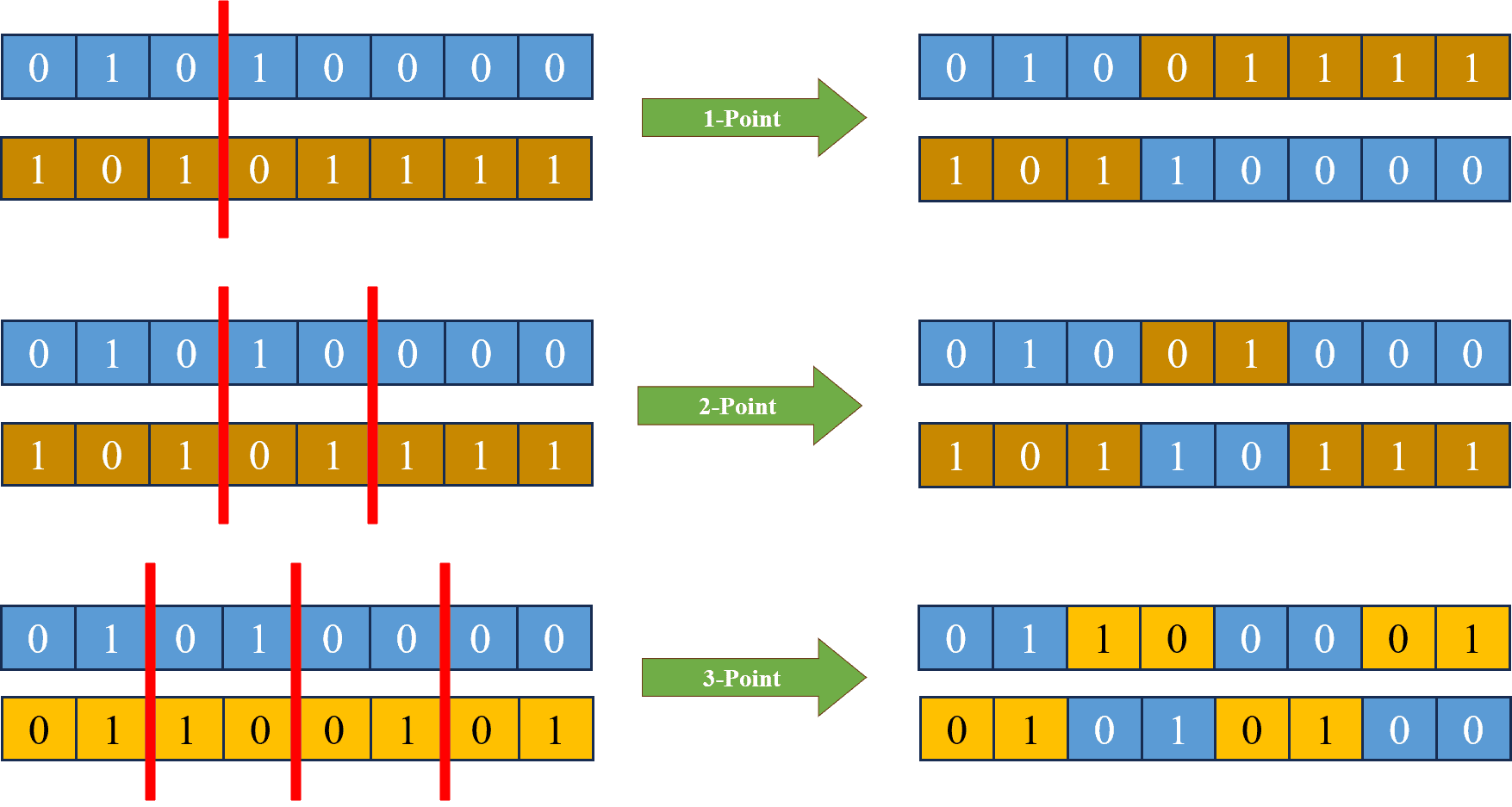 Hình 11: Minh hoạ một số phép lai trong giải thuật di truyền.
Hình 11: Minh hoạ một số phép lai trong giải thuật di truyền.
Tuy nhiên, để quá trình trao đổi chéo trở nên tự nhiên hơn, nghĩa là có thể xảy ra ở bất kỳ đâu trong một cá thể, chúng ta sẽ sử dụng Phép lai đồng nhất (Uniform Crossover), cụ thể như sau: Hoán đổi 2 ô ở cùng vị trí với xác suất cho trước. Hãy xem hình bên dưới để dễ hình dung hơn:
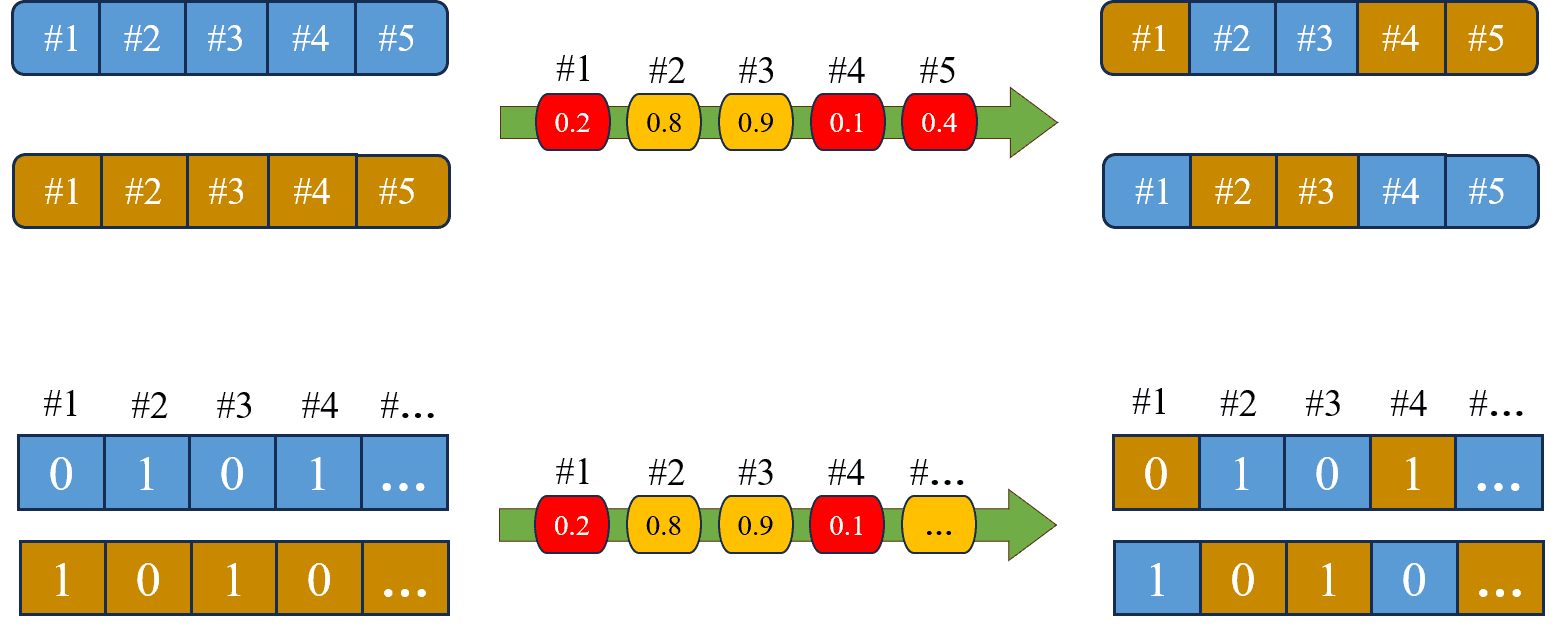 Hình 12: Minh hoạ Uniform Crossover.
Hình 12: Minh hoạ Uniform Crossover.
Quan sát Hình 12, giả sử ta cho trước xác suất hoán đổi là 0.5 và lấy các giá trị ngẫu nhiên trong khoảng từ cho các vị trí. Vị trí nào có giá trị nhỏ hơn hoặc bằng 0.5, ta sẽ hoán đổi tại vị trí đó.
Bước biến đổi tiếp theo chính là tạo sự đột biến cho cá thể con mới được tạo ra nhằm tạo sự đa dạng trong quần thể và tránh bị mắc kẹt ở các cực trị cục bộ. Để rõ hơn, hãy xem hình sau:
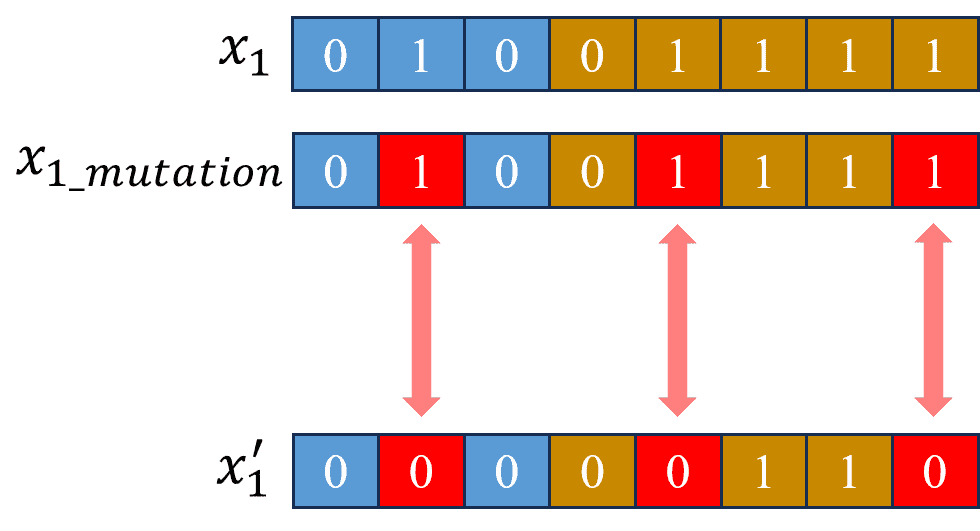 Hình 13: Đột biến cá thể x_1.
Hình 13: Đột biến cá thể x_1.
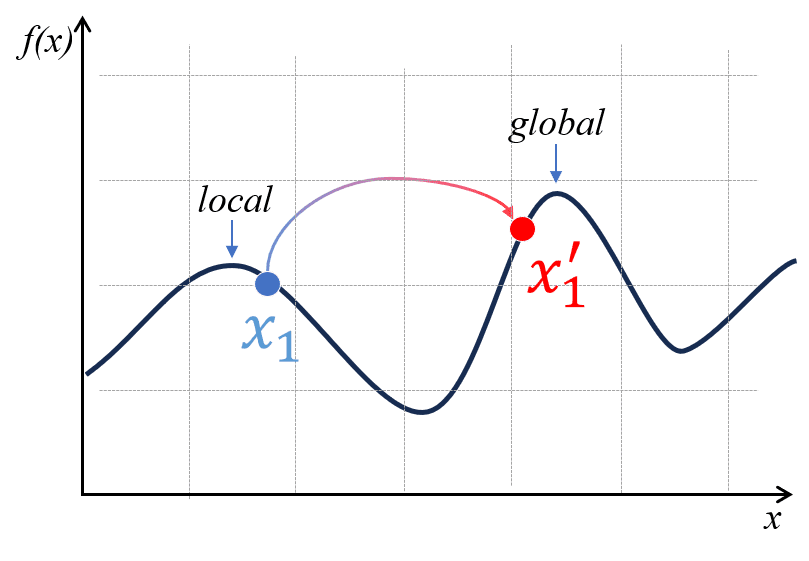 Hình 14: Tác động của việc đột biến.
Hình 14: Tác động của việc đột biến.
Minh họa về đột biến trong giải thuật di truyền.
Từ Hình 13, ta thấy cá thể bị đột biến ở các ô màu đỏ, vì bài toán của chúng ta giới hạn ở 2 giá trị 0 và 1, do đó, khi bị đột biến, nếu giá trị hiện tại của ô đó là 0 thì sẽ đổi thành 1 và ngược lại. Quan sát đồ thị ở Hình 14, ban đầu đang ở vùng cực đại cục bộ (local), nhưng nhờ bị đột biến và trở thành và nằm ở vùng cục đại toàn cục (global), giúp quá trình tối đa hoá Fitness đạt kết quả tối ưu hơn.
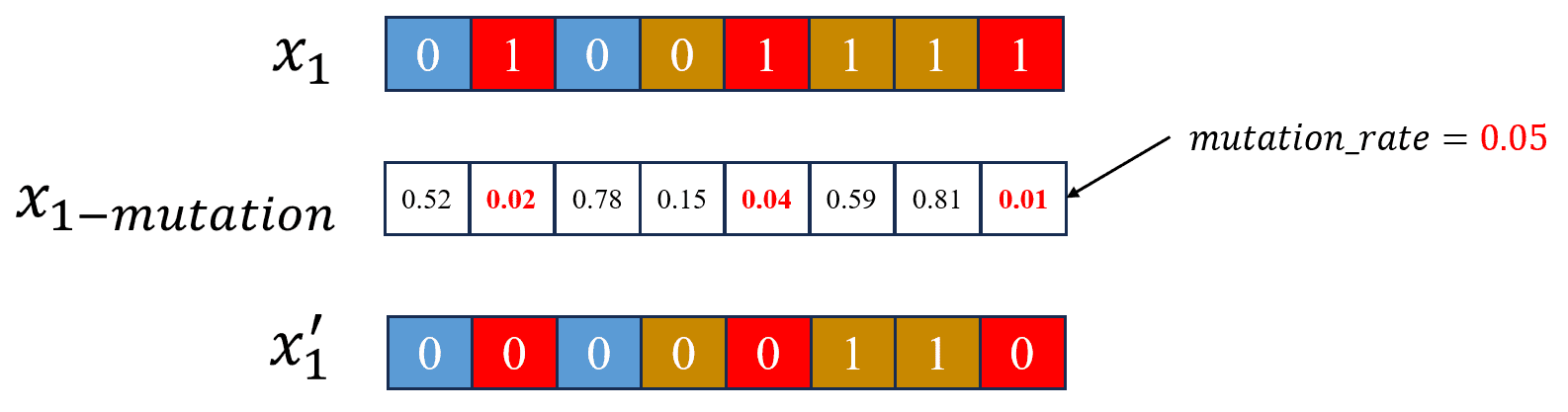 Hình 15: Minh hoạ việc mô phỏng đột biến trong giải thuật di truyền.
Hình 15: Minh hoạ việc mô phỏng đột biến trong giải thuật di truyền.
Để mô phỏng việc đột biến này, ta thực hiện tương tự như bước Crossover bằng cách chọn trước một ngưỡng, ví dụ như Hình 15, tiến hành lấy các giá trị ngẫu nhiên trong khoảng từ cho các vị trí, nếu vị trí nào có giá trị thấp hợp ngưỡng thì thực hiện đột biến tại vị trí đó.
Đây là bước cuối cùng, nhằm quyết định xem có tiếp tục tối ưu nữa không, hay kết thúc giải thuật di truyền. Một số tiêu chí để dừng thuật toán là:
Dựa theo cách triển khai đã đề cập ở phía trên, chúng ta sẽ thử áp dụng vào One-Max problem. Bài toán One-Max là một bài toán tối ưu đơn giản, trong đó mỗi cá thể là một chuỗi nhị phân gồm các giá trị 0 và 1. Mục tiêu của bài toán là tìm ra chuỗi nhị phân có số lượng số 1 lớn nhất, hay nói cách khác là tối đa hóa số lượng số 1 trong một chuỗi.
Công thức tính độ thích nghi (fitness) cho một cá thể được cho bởi:
trong đó: là các giá trị nhị phân của chuỗi .
Quá trình tối ưu hoá này diễn ra qua nhiều thế hệ, trong đó, ở mỗi thế hệ, các cá thể có độ thích nghi cao nhất (các cá thể ưu tú) sẽ được chọn lọc (selection) để tiếp tục vào vòng sau. Những cá thể không thuộc nhóm ưu tú sẽ tham gia vào quá trình lai ghép (crossover) và đột biến (mutation) để tạo ra thế hệ con, đảm bảo sự đa dạng và cải tiến cho quần thể. Bài toán sẽ được giải quyết qua nhiều thế hệ tiến hóa, với vòng lặp bắt đầu từ thế hệ đầu tiên và kết thúc sau một số lượng thế hệ nhất định. Trong trường hợp này, chúng ta đặt tham số , tức là sẽ thực hiện tiến hóa qua 5 thế hệ. Trong mỗi thế hệ, số lượng cá thể ưu tú (có độ thích nghi cao nhất) sẽ được giữ lại nguyên vẹn để tham gia vào thế hệ tiếp theo. Số lượng cá thể ưu tú được giữ lại sau mỗi thế hệ được xác định bởi tham số . Tham số này giúp duy trì những cá thể mạnh nhất, đồng thời tăng tốc độ tiến hoá của quần thể. Chiều dài của mỗi cá thể là , và kích thước quần thể được cố định ở mức , đảm bảo quá trình diễn ra ổn định và có thể theo dõi được sự tiến bộ qua từng thế hệ.
Bước đầu tiên trong GA là khởi tạo một quần thể ngẫu nhiên gồm các cá thể. Mỗi cá thể là một chuỗi nhị phân có chiều dài n, đại diện cho một lời giải khả thi. Số lượng cá thể trong quần thể được xác định bởi tham số m.
Đặt n = 5 và m = 5, chúng ta khởi tạo quần thể gồm 5 cá thể, mỗi cá thể có độ dài 5 bit. Các giá trị 0 và 1 trong mỗi cá thể được sinh ngẫu nhiên. Sau khi khởi tạo, quần thể sẽ trông như hình dưới đây:
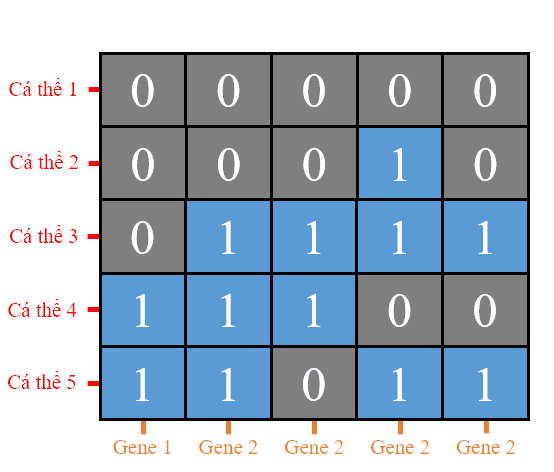 Hình 16: Quần thể khởi tạo ban đầu gồm 5 cá thể, mỗi cá thể là chuỗi nhị phân dài 5 bit.
Hình 16: Quần thể khởi tạo ban đầu gồm 5 cá thể, mỗi cá thể là chuỗi nhị phân dài 5 bit.
Như ta đã biết, công thức tính độ thích nghi (fitness) cho một cá thể được cho bởi:
Trong bài toán này, độ thích nghi (fitness) là tổng số lượng số 1 trong chuỗi nhị phân của mỗi cá thể. Vậy là sau khi đã có quần thể khởi tạo, ta đi tính độ thích nghi của quần thể của thế hệ hiện tại:
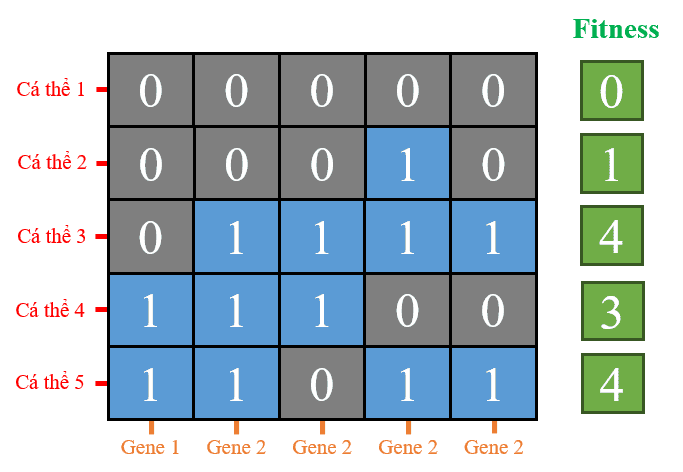 Hình 17: Minh họa tính độ thích nghi (fitness) của từng cá thể.
Hình 17: Minh họa tính độ thích nghi (fitness) của từng cá thể.
Bước chọn lọc sẽ chọn ra các cá thể có độ thích nghi cao hơn để tham gia vào các bước lai ghép tiếp theo. Ta thực hiện chọn lọc dựa trên độ thích nghi (fitness). Ở đây, elitism = 2, nghĩa là hai cá thể có độ thích nghi cao nhất sẽ được giữ lại mà không thay đổi. Xét ở quần thể hiện tại, hai cá thể này là:
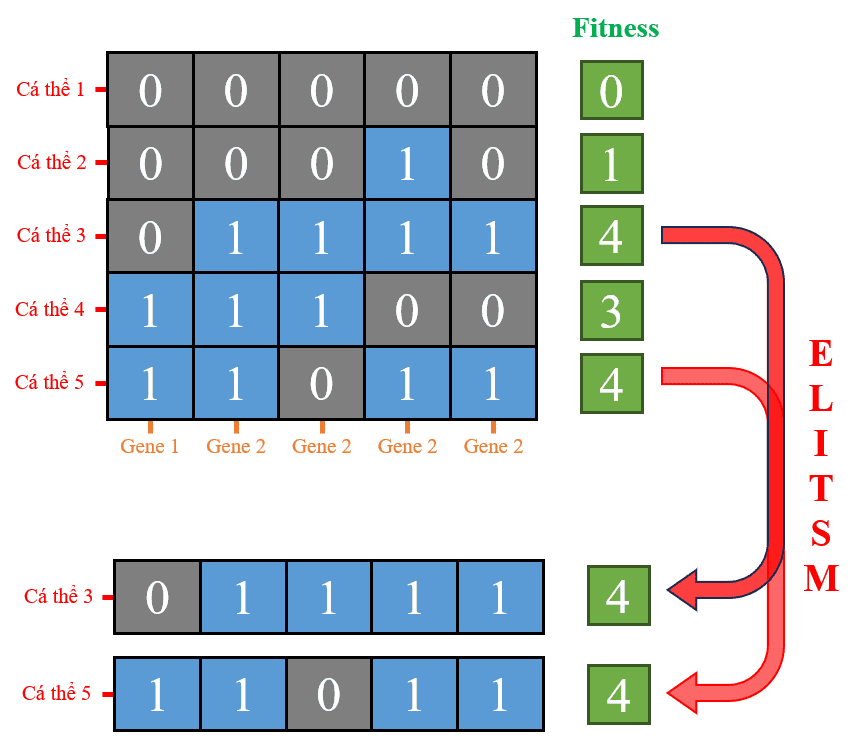 Hình 18: Minh họa quá trình chọn lọc ra các cá thể có độ thích nghi cao nhất.
Hình 18: Minh họa quá trình chọn lọc ra các cá thể có độ thích nghi cao nhất.
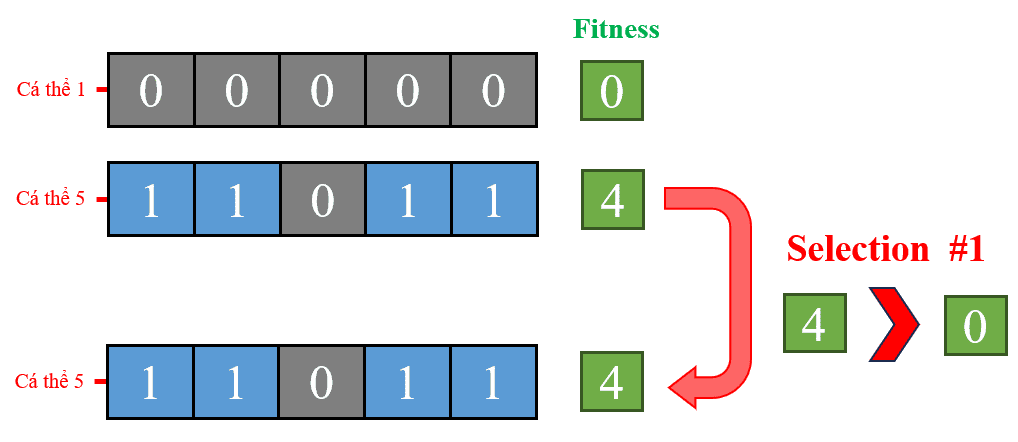 Hình 19: Quá trình chọn lọc lần 1 giữa cá thể 1 và cá thể 5.
Hình 19: Quá trình chọn lọc lần 1 giữa cá thể 1 và cá thể 5.
Sau đó, chúng ta tiến hành chọn ngẫu nhiên hai cá thể từ quần thể để so sánh độ thích nghi của chúng. Trong lần chọn thứ nhất, cá thể 1 (fitness = 0) và cá thể 5 (fitness = 4) được chọn ngẫu nhiên để so sánh. Vì cá thể 5 có fitness cao hơn, nó được giữ lại để tham gia vào quá trình lai ghép, còn cá thể 1 do có độ thích nghi thấp nên bị loại bỏ.
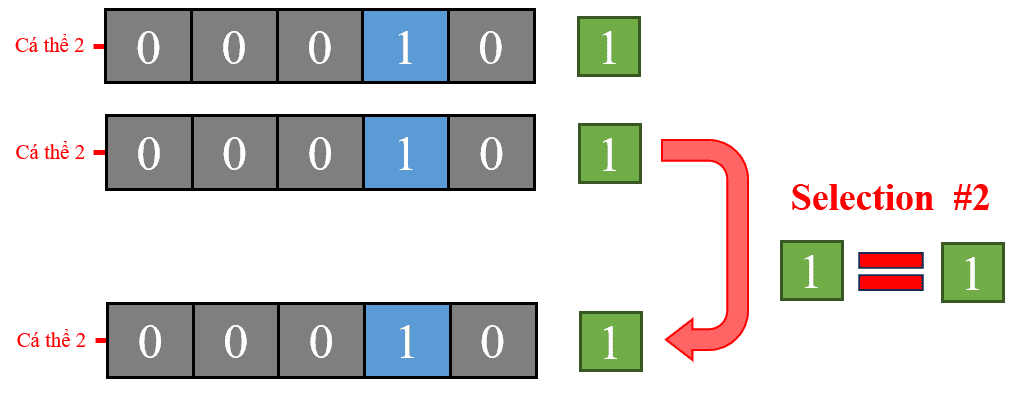 Hình 20: Quá trình chọn lọc lần 2 giữa cá thể 2 cá thể giống nhau.
Hình 20: Quá trình chọn lọc lần 2 giữa cá thể 2 cá thể giống nhau.
Ta thực hiện tìm cá thể cha mẹ còn lại. Theo đó, hai cá thể giống nhau (cùng là cá thể 2) với fitness = 1 được chọn ngẫu nhiên để so sánh. Kết quả không thay đổi và cá thể 2 sẽ được giữ lại do đây là cá thể duy nhất trong lần chọn này. Mặc dù hai cá thể giống nhau đã được chọn ngẫu nhiên trong quá trình chọn lọc, nhưng quá trình này vẫn được thực hiện để đảm bảo tính ngẫu nhiên và tính đa dạng di truyền trong quần thể.
Sau quá trình chọn lọc, các cá thể tốt nhất được giữ lại để tiếp tục tham gia vào quá trình tiến hóa trong thế hệ tiếp theo. Cụ thể, ở thế hệ hiện tại, ta đã chọn ra được:
Tiếp theo, chúng ta thực hiện quá trình lai ghép (crossover) để tạo ra các cá thể con từ những cá thể được chọn lọc. Quá trình lai ghép được thực hiện theo phương pháp lai ghép đồng nhất (uniform crossover), trong đó mỗi gene của cá thể cha có xác suất 0.9 để hoán đổi với gene tương ứng của cá thể mẹ. Bằng cách tạo giá trị ngẫu nhiên cho mỗi vị trí gene, ta thực hiện so sánh nếu nhỏ hơn ngưỡng 0.9 thì việc hoán đổi gene sẽ được thực hiện như hình dưới đây:
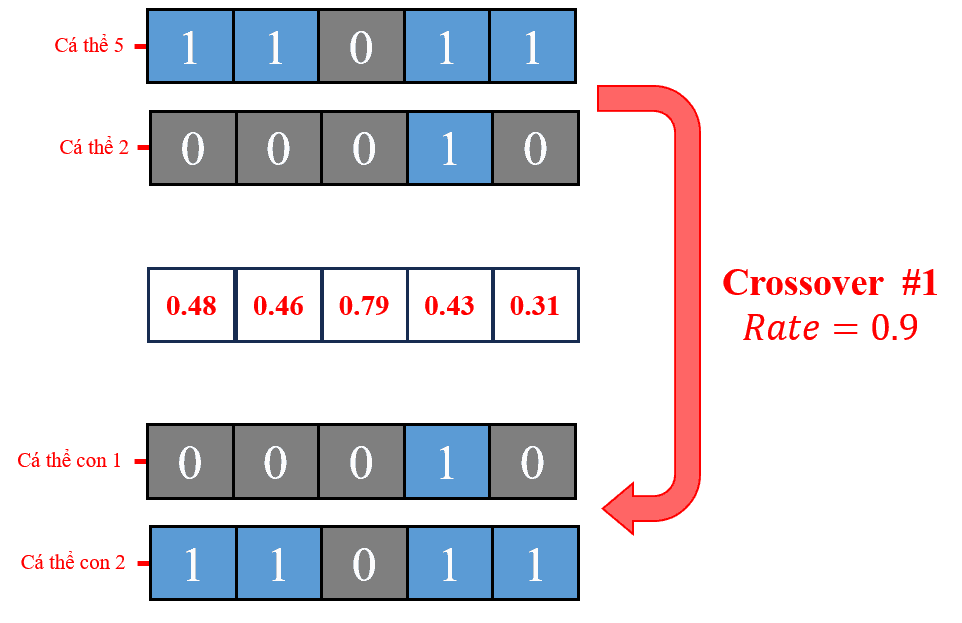 Hình 21: Quá trình lai ghép tạo ra các cá thể con từ những cá thể được chọn lọc.
Hình 21: Quá trình lai ghép tạo ra các cá thể con từ những cá thể được chọn lọc.
Ta có:
Do tất cả các giá trị ngẫu nhiên sinh ra đều nhỏ hơn 0.9, nên tất cả các gene của cá thể cha và cá thể mẹ sẽ được hoán đổi. Điều này dẫn đến kết quả của hai cá thể con sẽ là sự hoán đổi toàn bộ các gene giữa cá thể cha và mẹ.
Kết quả sau khi lai ghép tạo ra hai cá thể con mới:
Trong bước đột biến, chúng ta áp dụng xác suất đột biến cho từng gene của các cá thể con vừa được tạo ra ở bước lai ghép trên. Với xác suất 5% (0.05), mỗi gene trong chuỗi nhị phân có thể bị thay đổi. Điều này có nghĩa là một gene có thể chuyển từ ’0’ thành ’1’ hoặc ngược lại, từ ’1’ thành ’0’. Về cách thực hiện, ta áp dụng cách làm tương tự như phép lai đồng nhất - tạo ra giá trị ngẫu nhiên cho từng gene và thực hiện so sánh với giá trị ngưỡng như hình sau:
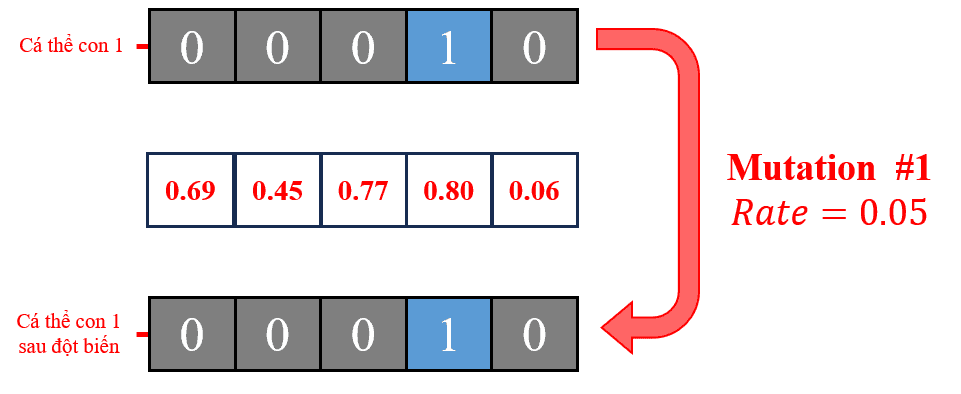 Hình 22: Quá trình đột biến cá thể con 1.
Hình 22: Quá trình đột biến cá thể con 1.
Do các giá trị ngẫu nhiên sinh ra đều lớn hơn 0.05, cá thể con 1 không có gene nào bị thay đổi trong quá trình đột biến. Kết quả là cá thể con 1 vẫn giữ nguyên với gene [0, 0, 0, 1, 0].
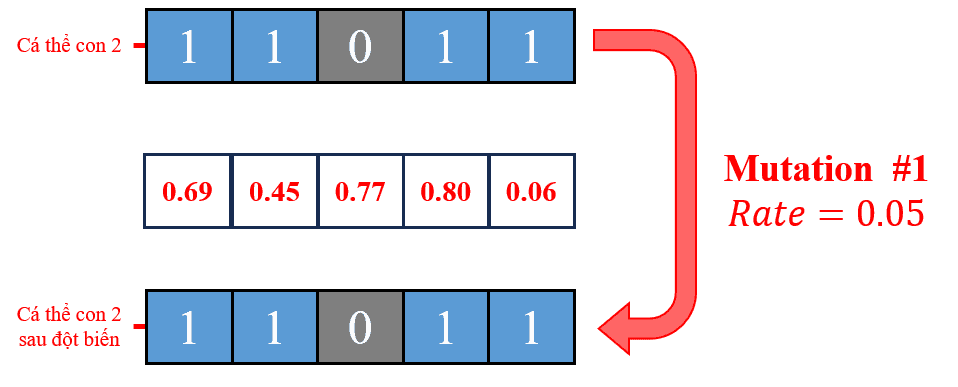 Hình 23: Quá trình đột biến cá thể con 2.
Hình 23: Quá trình đột biến cá thể con 2.
Tương tự như cá thể con 1, cá thể con 2 cũng không có gene nào bị thay đổi và giữ nguyên giá trị gene [1, 1, 0, 1, 1].
Đến cuối phần 5 (Mutation), chúng ta đã hoàn thành các bước lai ghép (Crossover) và đột biến (Mutation) cho thế hệ thứ nhất. Sau bước lai ghép, hai cá thể con mới đã được tạo ra từ các cá thể cha mẹ với gene được hoán đổi theo xác suất 0.9. Kết quả của hai cá thể con là:
Tiếp theo, ở bước đột biến, giá trị ngẫu nhiên sinh ra cho cả hai cá thể đều lớn hơn 0.05, do đó không có gene nào bị thay đổi trong quá trình đột biến. Vì vậy, sau khi đột biến, các cá thể vẫn giữ nguyên cấu trúc như sau:
Như vậy, đến thời điểm này, chúng ta đã hoàn tất việc lai ghép và đột biến cho hai cá thể con mới, và chúng đã sẵn sàng để thêm vào quần thể của thế hệ thứ nhất. Tuy nhiên, số lượng cá thể trong quần thể hiện tại sau Mutation vẫn chưa đủ để hoàn chỉnh quần thể thế hệ 1 (vì ). Vì vậy, bước tiếp theo sẽ là quay lại phần chọn lọc (Selection) một lần nữa để chọn thêm các cá thể và bổ sung vào quần thể mới. Điều này sẽ giúp đảm bảo quần thể thế hệ 1 có đầy đủ số lượng cá thể cần thiết.
Đến đây, dù đã hoàn tất các bước lai ghép và đột biến, nhưng vẫn chưa hoàn chỉnh toàn bộ thế hệ mới (thế hệ 1) vì số lượng cá thể trong quần thể mới vẫn chưa đủ. Ta cần quay lại phần chọn lọc (Selection) thêm một lần nữa để hoàn chỉnh quần thể cho thế hệ 1 bằng cách bổ sung thêm các cá thể phù hợp. Việc này là cần thiết để đảm bảo quần thể có đầy đủ số cá thể như ban đầu (m = 5).
Sau quá trình đột biến, ta đã có hai có thể con mới. Song, nhận thấy số lượng cá thể của quần thể hiện tại đang là 4 (gồm hai cá thể tinh anh và hai cá thể con), nhỏ hơn số kích thước quần thể mà chúng ta đã định nghĩa ban đầu. Vì vậy, để thỏa mãn kích thước quần thể, ta chạy lại một lần nữa việc chọn lọc, lai ghép và đột biến. Vì đây chỉ là các bước lặp lại tương tự mô tả trên, kết quả của lần lặp lại này sẽ được mô tả thông qua hình ảnh:
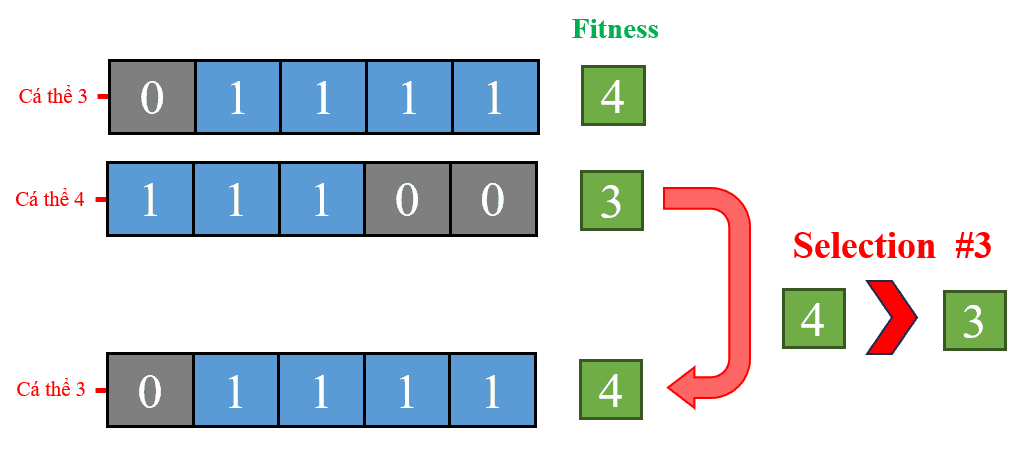 Hình 24: Chọn lọc lần thứ 2: Giữa cá thể 3 và 4 trong quần thể ban đầu, cá thể 3 được chọn do có độ thích nghi cao hơn.
Hình 24: Chọn lọc lần thứ 2: Giữa cá thể 3 và 4 trong quần thể ban đầu, cá thể 3 được chọn do có độ thích nghi cao hơn.
Ở lần chọn lọc này, cá thể 3 và cá thể 4 được đưa vào cạnh tranh, với độ thích nghi lần lượt là 4 và 3. Cá thể có độ thích nghi cao hơn (cá thể 3) sẽ được giữ lại trong quần thể thế hệ 1.
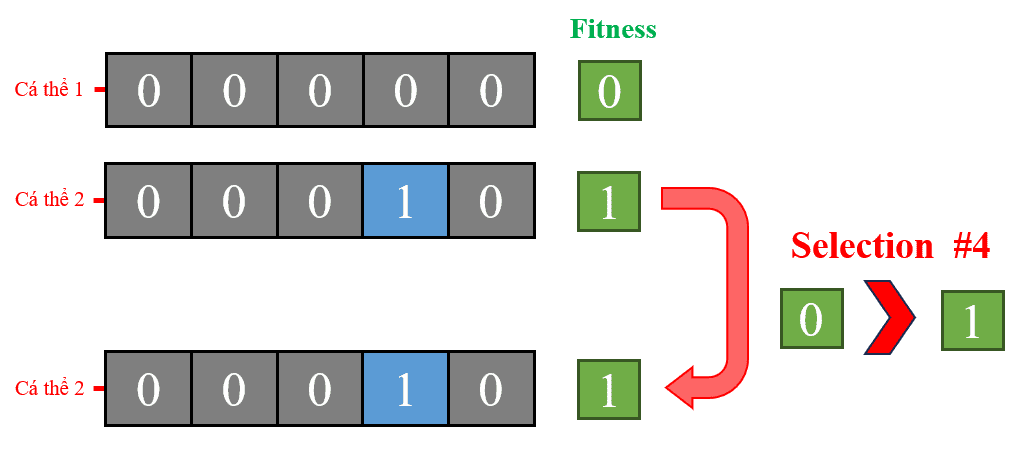 Hình 25: Chọn lọc lần thứ 2: Giữa cá thể 1 và 2 trong quần thể ban đầu, cá thể 2 được chọn do có độ thích nghi cao hơn.
Hình 25: Chọn lọc lần thứ 2: Giữa cá thể 1 và 2 trong quần thể ban đầu, cá thể 2 được chọn do có độ thích nghi cao hơn.
Tương tự, cá thể 1 và cá thể 2 được so sánh, với độ thích nghi lần lượt là 0 và 1. Kết quả là cá thể 2, có độ thích nghi cao hơn, được chọn giữ lại.
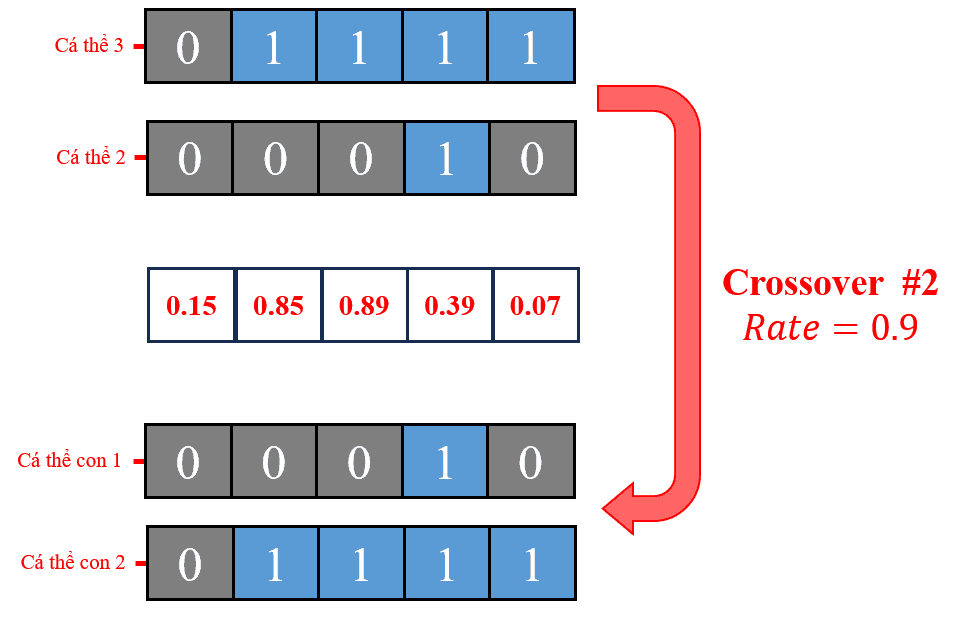 Hình 26: Lai ghép lần thứ 2: Với hai cá thể cha mẹ được chọn từ lần chọn lọc thứ 2, thực hiện phép lai đồng nhất để tạo ra hai cá thể con mới.
Hình 26: Lai ghép lần thứ 2: Với hai cá thể cha mẹ được chọn từ lần chọn lọc thứ 2, thực hiện phép lai đồng nhất để tạo ra hai cá thể con mới.
Quá trình lai ghép đồng nhất được thực hiện giữa cá thể cha mẹ thứ 3 và cá thể cha mẹ thứ 2. Trong quá trình này, mỗi gene của cá thể con có xác suất nhỏ hơn 0.9 được hoán đổi với gene tương ứng từ cá thể cha mẹ. Do các giá trị ngẫu nhiên sinh ra cho từng gene đều nhỏ hơn 0.9, tất cả các gene của hai cá thể cha mẹ được hoán đổi hoàn toàn cho nhau. Kết quả là hai cá thể con mới được tạo ra với cấu trúc gene như trong Hình 26.
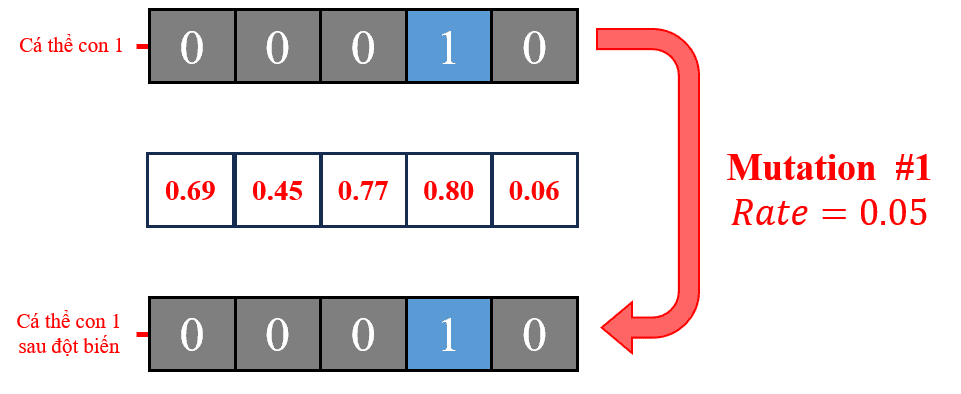 Hình 27: Đột biến lần thứ 1: Thực hiện đột biến cá thể con 1 vừa được tạo ra từ việc lai ghép lần 2.
Hình 27: Đột biến lần thứ 1: Thực hiện đột biến cá thể con 1 vừa được tạo ra từ việc lai ghép lần 2.
Đối với cá thể con 1 có chuỗi gene ban đầu là [0, 0, 0, 1, 0], tất cả các giá trị này đều lớn hơn 0.05, không có sự thay đổi gene nào xảy ra. Do đó, cá thể con 1 sau quá trình đột biến vẫn giữ nguyên chuỗi gene là [0, 0, 0, 1, 0].
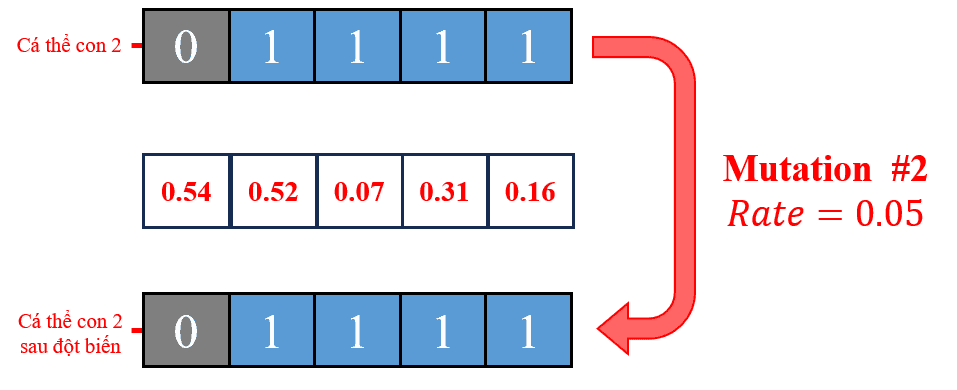 Hình 28: Đột biến lần thứ 2: Thực hiện đột biến cá thể con 2 vừa được tạo ra từ việc lai ghép lần 2.
Hình 28: Đột biến lần thứ 2: Thực hiện đột biến cá thể con 2 vừa được tạo ra từ việc lai ghép lần 2.
Tương tự, đối với cá thể con 2 có chuỗi gene ban đầu là [0, 1, 1, 1, 1], các giá trị ngẫu nhiên được sinh ra đều lớn hơn 0.05, do đó, không có sự thay đổi gene nào xảy ra. Kết quả là cá thể con 2 sau quá trình đột biến vẫn giữ nguyên chuỗi gene.
Vì kích thước quần thể cho thế hệ mới hiện tại đã là 4, tức với hai cá thể con vừa được tạo ra, ta chỉ được đưa một trong hai vào quần thể mới. Khi đã thỏa mãn kích thước của quần thể, ta có một quần thể của thế hệ mới như sau:
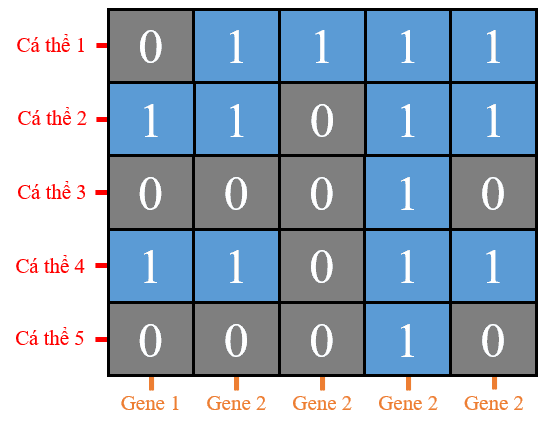 Hình 29: Quần thể mới tạo ra sau quá trình chọn lọc, lai ghép và đột biến từ quần thể ban đầu.
Hình 29: Quần thể mới tạo ra sau quá trình chọn lọc, lai ghép và đột biến từ quần thể ban đầu.
Như vậy, quần thể mới sau thế hệ 1 bao gồm các cá thể có độ fitness khác nhau, nhưng vẫn duy trì các cá thể mạnh nhất và đảm bảo số lượng cá thể không thay đổi. Hình 29 minh họa sự sắp xếp của quần thể sau khi thực hiện quá trình đột biến và lai ghép.
Các bước thực hiện trên là dành cho một thế hệ. Vì ta cài đặt số thế hệ là 5, các bước trên sẽ được lặp lại thêm 4 lần để tìm ra cá thể có độ thích nghi cao nhất cho bài toán One-max này. Theo đó, quần thể tại thế hệ cuối cùng (thế hệ thứ 5) sẽ có kết quả như hình sau:
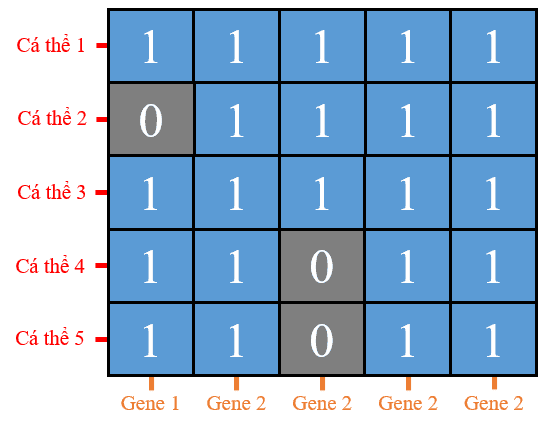 Hình 30: Quần thể tại thế hệ cuối cùng (thế hệ thứ 5).
Hình 30: Quần thể tại thế hệ cuối cùng (thế hệ thứ 5).
Dựa vào thông tin độ thích nghi tốt nhất qua từng thế hệ, ta cũng có thể trực quan rõ hơn sự cải thiện của cá thể tốt nhất (lời giải tốt nhất) qua từng thế hệ hệ trên đồ thị như sau:
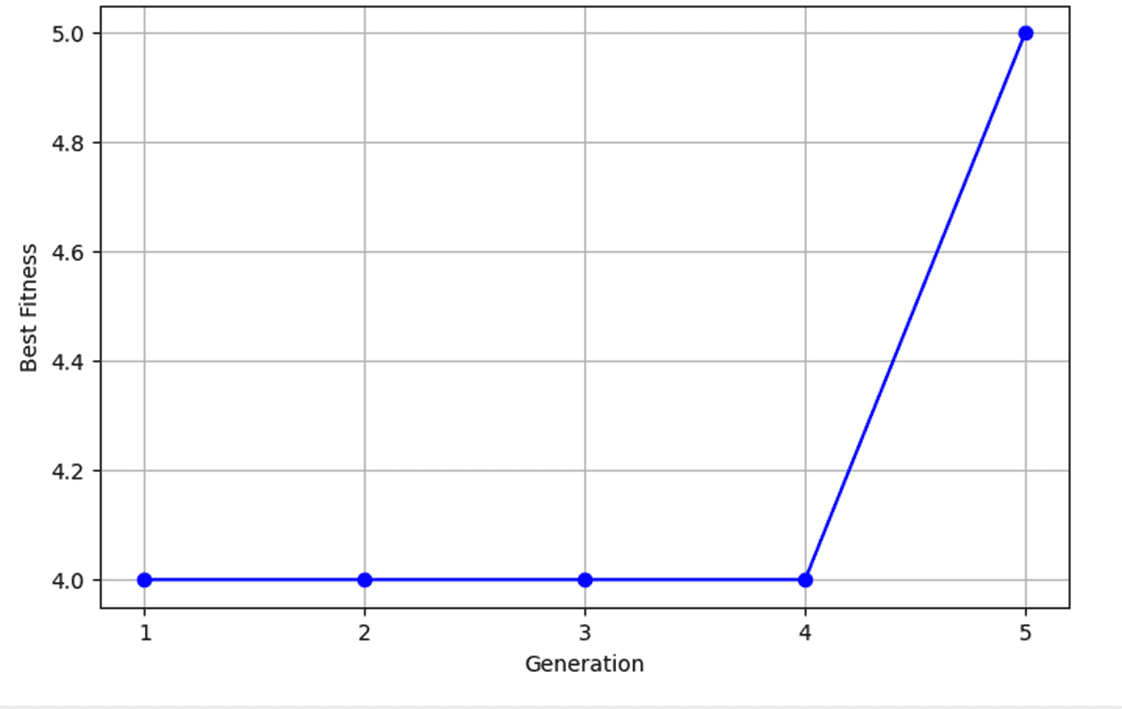 Hình 31: Sự tiến hóa của độ thích nghi tốt nhất qua các thế hệ.
Hình 31: Sự tiến hóa của độ thích nghi tốt nhất qua các thế hệ.
- Hết -