Tác giả: Anh-Khoi Nguyen (AIO2024), Dinh-Thang Duong (TA), Phuc-Thinh Nguyen (AIO2024, CM), Quang-Vinh Dinh (Lecturer)
Keywords: hồi quy tuyến tính, step by step linear regression, học ai online
Hãy tưởng tượng chúng ta có một bài toán như sau: Xây dựng một chương trình tự động dự đoán tiền lương của nhân viên dựa trên số năm kinh nghiệm của họ. Để trực quan hóa, ta gọi số năm kinh nghiệm là và số tiền lương là . Khi đó, với một vài thông tin cho trước của một vài nhân viên, ta có thể sử dụng trục đồ thị Oxy để trực quan hóa dữ liệu như hình sau:
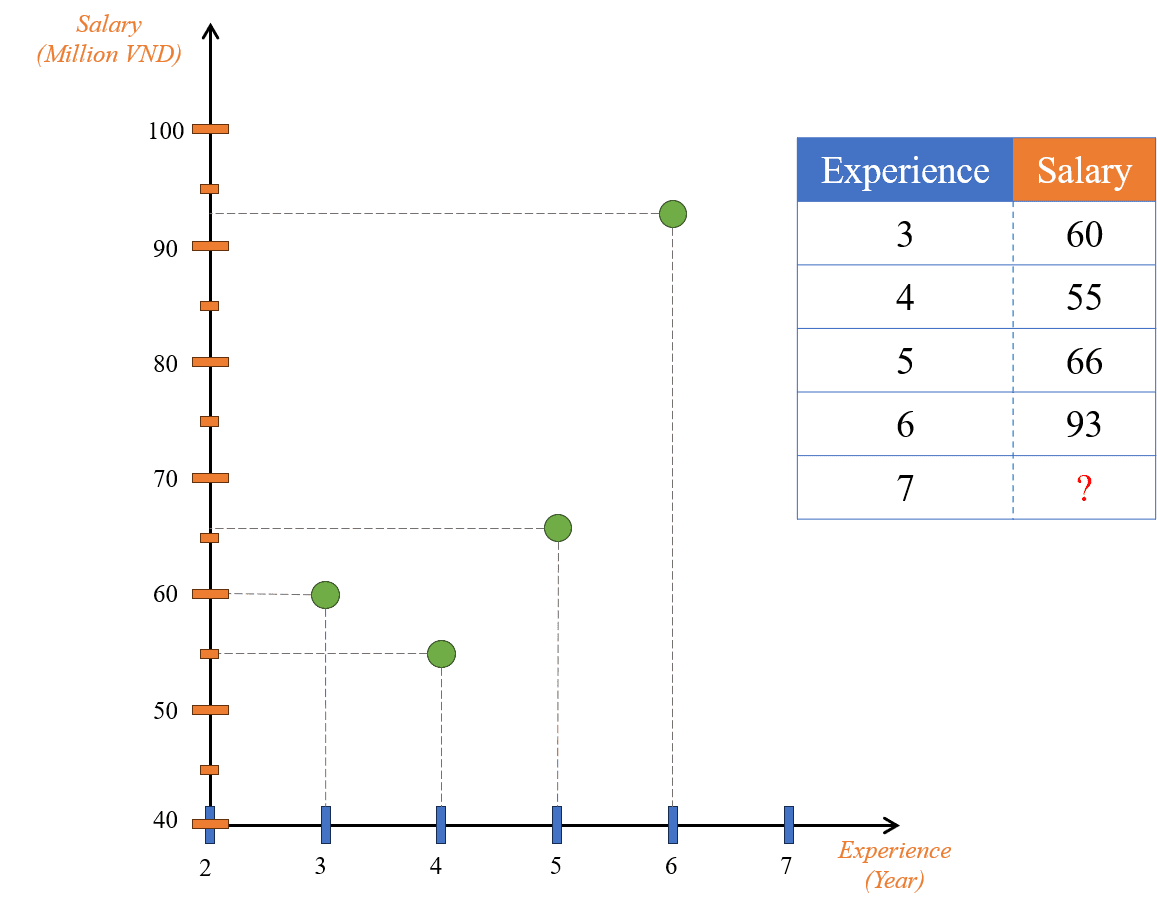 Hình 1: Minh họa dữ liệu tiền lương theo số năm kinh nghiệm trên đồ thị.
Hình 1: Minh họa dữ liệu tiền lương theo số năm kinh nghiệm trên đồ thị.
Câu hỏi đặt ra là, làm cách nào để ta có thể code một chương trình có thể tự động dự đoán tiền lương dựa vào số năm kinh nghiệm? Quan sát thấy rằng, khi ta dùng một đường vẽ ngang qua một điểm dữ liệu, ta thực chất có thể dùng phương trình đường thẳng này để dự đoán được chính xác tiền lương của nhân viên ứng với số năm kinh nghiệm của họ.
Như vậy, với một đường thẳng bất kỳ, ta hoàn toàn có thể dùng nó cho "chương trình" dự đoán tiền lương. Khi xét một phương trình đường thẳng , có thể thấy mỗi đường thẳng khác nhau sẽ có số và khác nhau (1).
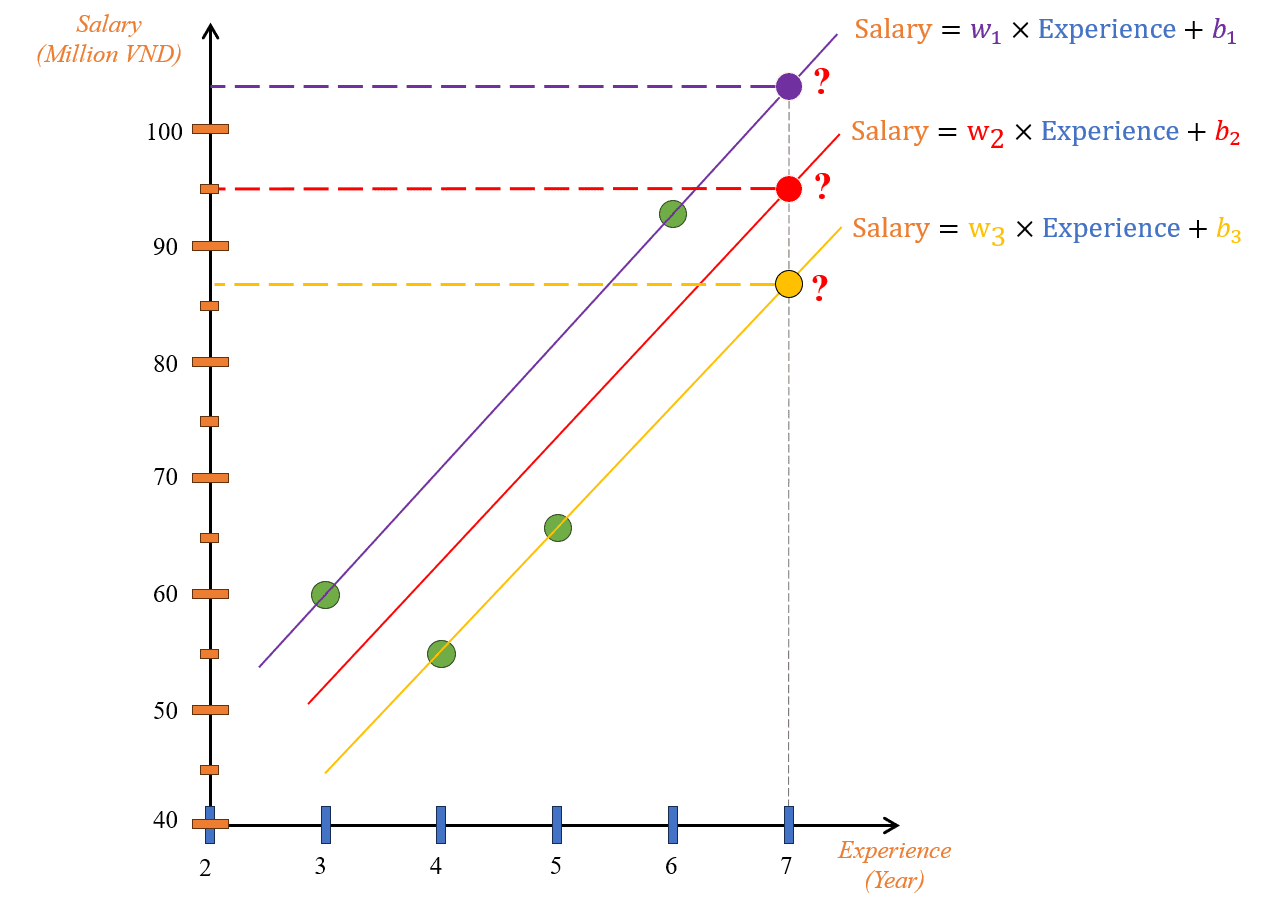 Hình 3: Các giá trị w và b khác nhau sẽ cho ta các đường thẳng khác nhau.
Hình 3: Các giá trị w và b khác nhau sẽ cho ta các đường thẳng khác nhau.
Quan sát Hình 3, đường thẳng trên cùng (màu tím) đi qua 2 điểm (Experience=3, Salary=60) và (6, 93); đường thẳng dưới cùng (màu vàng) đi qua 2 điểm (4, 55) và (5, 66); đường thẳng màu đỏ nằm giữa 2 đường thẳng trên và không đi qua bất kỳ điểm nào.
Mặc dù không thể nào vẽ được một đường thẳng có thể dự đoán chính xác toàn bộ các điểm cho trước. Tuy nhiên, từ quan sát này, với các điểm dữ liệu cho trước như vậy, liệu rằng chúng ta có thể vẽ được một đường thẳng mà có thể xấp xỉ được gần đúng các điểm dữ liệu hiện có hay không?
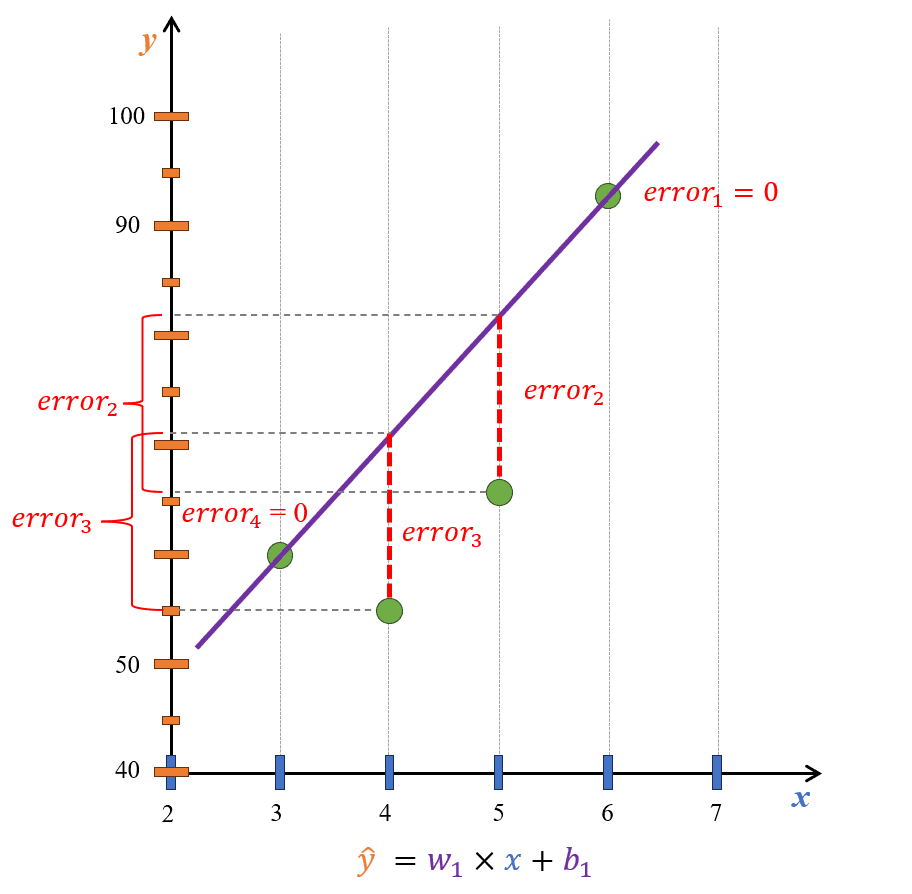 Hình 4: Khoảng cách từ một điểm đến một đường thẳng trong ngữ cảnh Linear Regression thường được gọi là error.
Hình 4: Khoảng cách từ một điểm đến một đường thẳng trong ngữ cảnh Linear Regression thường được gọi là error.
Để tìm được một đường thẳng xấp xỉ tối ưu nhất, ta có thể nghĩ theo hướng rằng, khoảng cách từ các điểm trong đồ thị đến đường thẳng đó phải là ngắn nhất. Ta sẽ tạm gọi tổng các khoảng cách này với một cái tên là loss.
Tiếp theo, chúng ta sẽ xem xét các giá trị có thể thay đổi để khiến loss giảm, xét vế phải của phương trình đường thẳng , với là dữ liệu đầu vào nên sẽ không thay đổi được. Vì vậy, ta chỉ có thể thay đổi 2 giá trị và để khiến loss giảm đi, sau đây là 2 hình ảnh trực quan cho các đường thẳng với các giá trị và khác nhau (được thay đổi theo một hướng tích cực mà chúng ta sẽ tìm hiểu ở các phần sau trong bài đọc này) và giá trị loss tương ứng với đường thẳng đó:
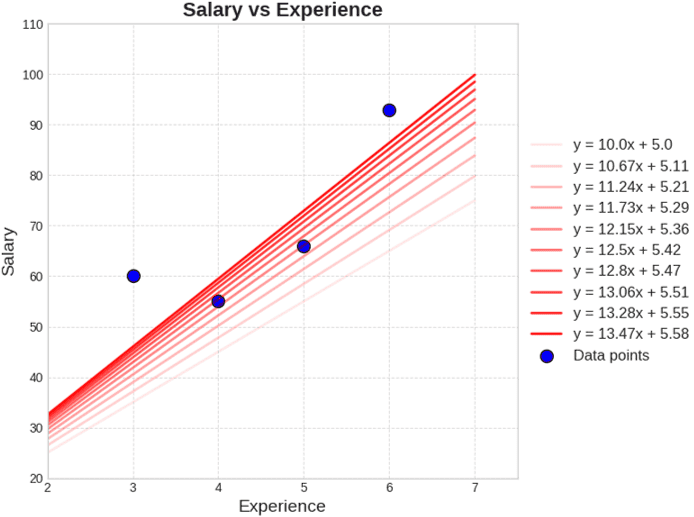 Hình 5: Các đường thẳng với giá trị w và b khác nhau.
Hình 5: Các đường thẳng với giá trị w và b khác nhau.
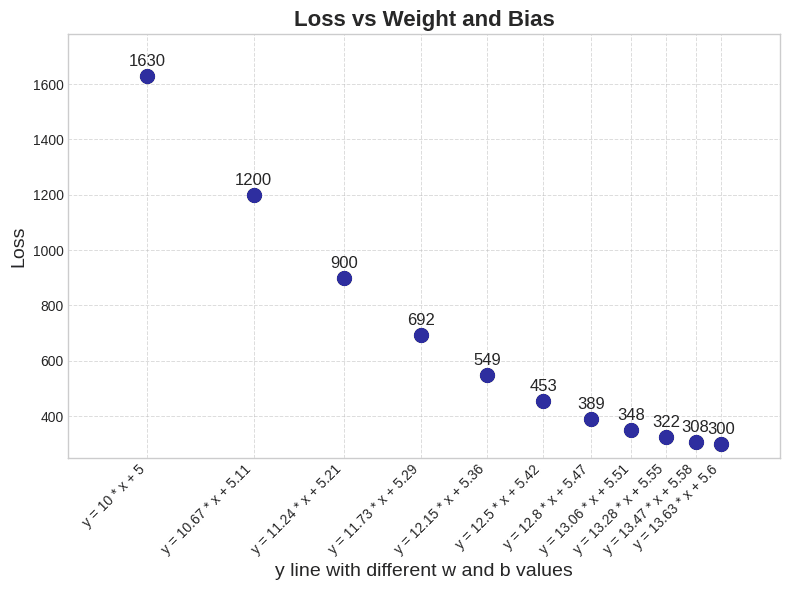 Hình 6: Tổng khoảng cách giữa các điểm đến đường thẳng tương ứng của mỗi đường thẳng.
Hình 6: Tổng khoảng cách giữa các điểm đến đường thẳng tương ứng của mỗi đường thẳng.
Có thể thấy rằng tại Hình 6, khi giá trị và thay đổi dần theo một hướng "tích cực" thì loss sẽ giảm dần; cho đến khi và là một giá trị phù hợp sẽ tạo ra một đường thẳng tối ưu nhất (đường thẳng đậm nhất trong Hình 5) cho các dữ liệu đang xét và khiến giá trị loss cũng đạt giá trị nhỏ nhất (như đường thẳng với và thì có loss nhỏ nhất ) (2).
Từ (1) và (2), ta có một bài toán mới được phát biểu như sau: Tìm và để giá trị loss là nhỏ nhất. Để đơn giản và dễ hiểu, chúng ta sẽ xét riêng giá trị , các bạn có thể nhìn hình dưới đây:
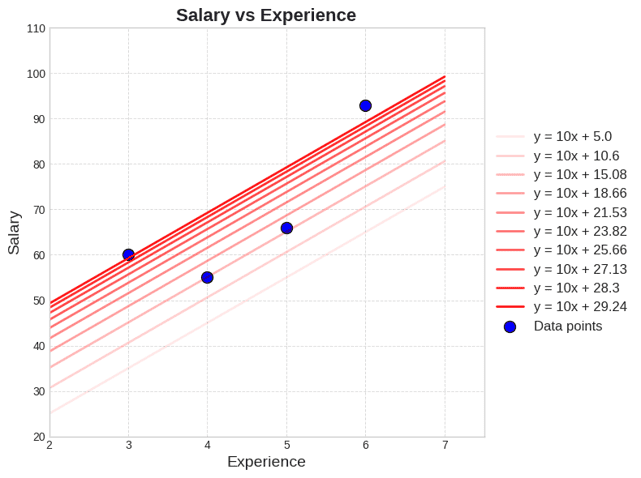 Hình 7: Các đường thẳng với giá trị b khác nhau.
Hình 7: Các đường thẳng với giá trị b khác nhau.
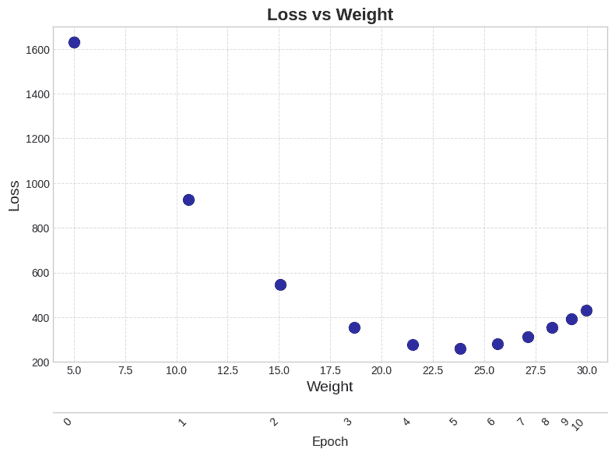 Hình 8: Tổng khoảng cách giữa các điểm đến đường thẳng tương ứng của mỗi đường thẳng.
Hình 8: Tổng khoảng cách giữa các điểm đến đường thẳng tương ứng của mỗi đường thẳng.
Xét cụ thể theo ví dụ trong hình, làm cách nào để ta có thể tìm được giá trị tối ưu sao cho loss là nhỏ nhất? Giả sử ta có phương trình khoảng cách giữa và là , với là giá trị đúng hay nhãn cho giá trị đầu vào và là một phương trình đường thẳng bất kỳ, nhận đầu vào là và dự đoán giá trị mới. Để tìm giá trị tối ưu cho các dữ liệu để hàm loss nhỏ nhất, ta sẽ cố định giá trị của w và chỉ thay đổi giá trị và có thể trực quan mối quan hệ giữa loss và như sau:
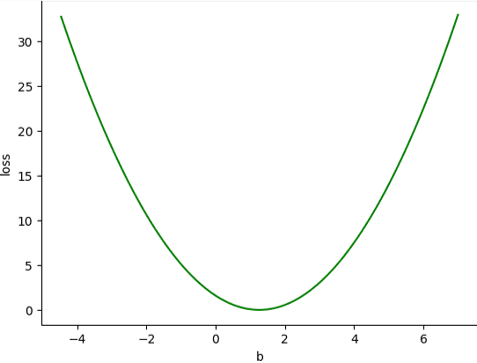 Hình 9: Thay đổi giá trị b trong khi giữ nguyên giá trị w.
Hình 9: Thay đổi giá trị b trong khi giữ nguyên giá trị w.
Quan sát thấy, hàm loss của chúng ta lúc này là một đường parabol, và vị trí cực tiểu biểu trưng cho giá trị loss nhỏ nhất. Vậy chẳng phải lúc này nếu ta bằng một cách nào đó có thể tìm được giá trị tại điểm cực tiểu này, ta sẽ tìm được đường thẳng có loss là thấp nhất không? Nhưng làm cách nào để ta có thể tự động tìm ra được giá trị tối ưu này?
Nói một cách khác, nếu coi giá trị bias ta có ban đầu là một điểm nằm trên hàm loss, làm cách nào để ta có thể di chuyển điểm đó tiến về phía cực tiểu?
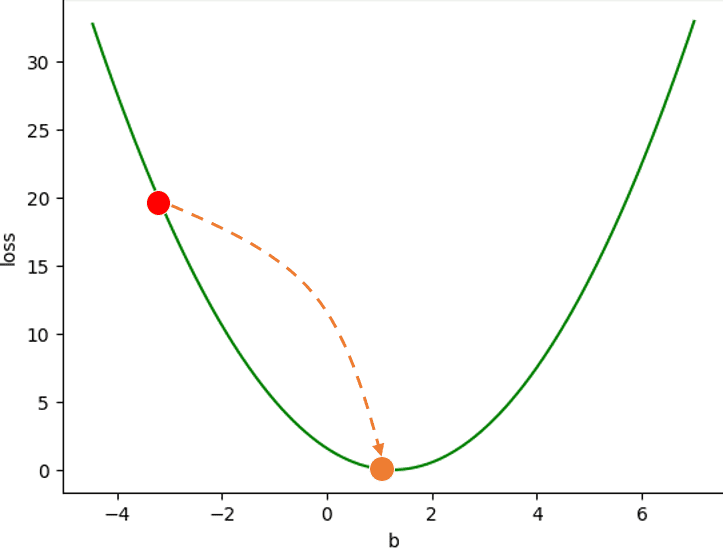 Hình 10: Di chuyển b đến vị trí làm cho hàm loss đạt cực tiểu.
Hình 10: Di chuyển b đến vị trí làm cho hàm loss đạt cực tiểu.
Để hiện thực được ý tưởng này, chúng ta có thể sử dụng công cụ đạo hàm. Nhắc qua một chút về khái niệm đạo hàm, khi chúng ta có giá trị đạo hàm tại một vị trí trên hàm số, chúng ta sẽ biết được thông tin về độ dốc của hàm tại điểm đó, biểu thị bằng đường tiếp tuyến tại một điểm, như hình dưới đây:
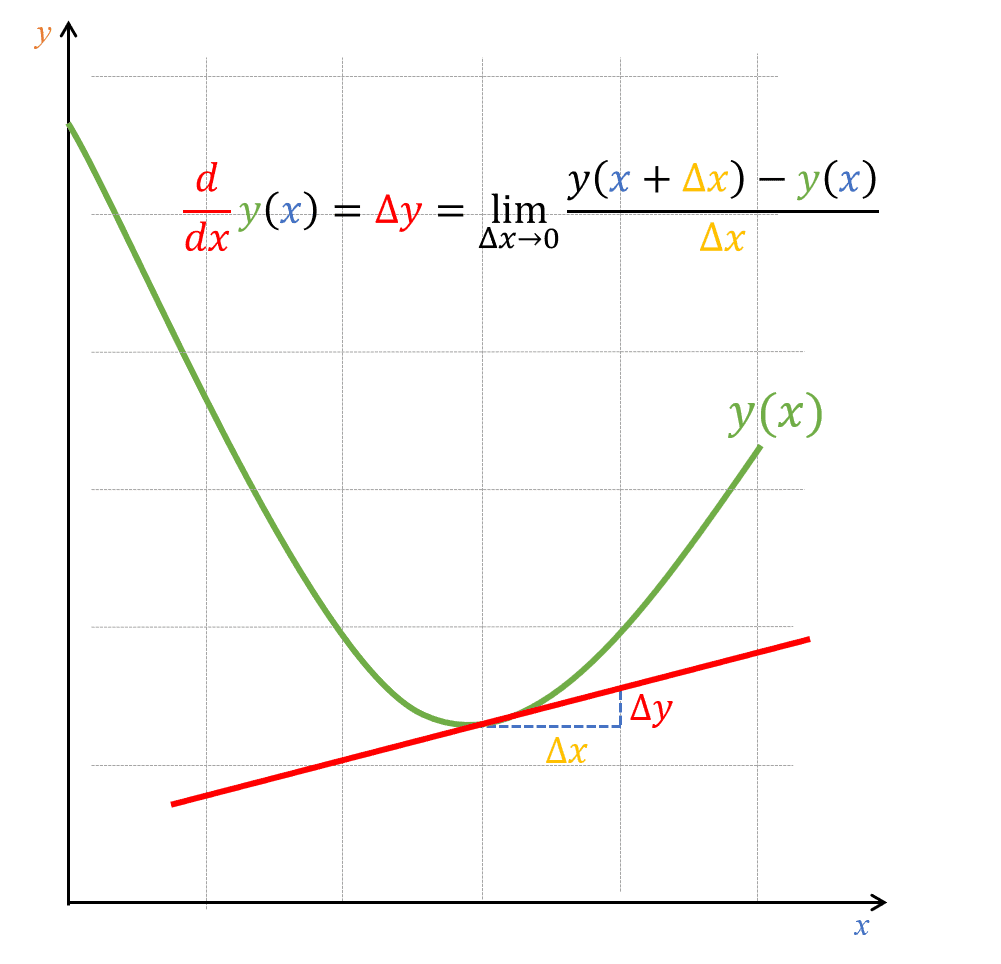 Hình 11: Đường tiếp tuyến của một hàm tại một điểm.
Hình 11: Đường tiếp tuyến của một hàm tại một điểm.
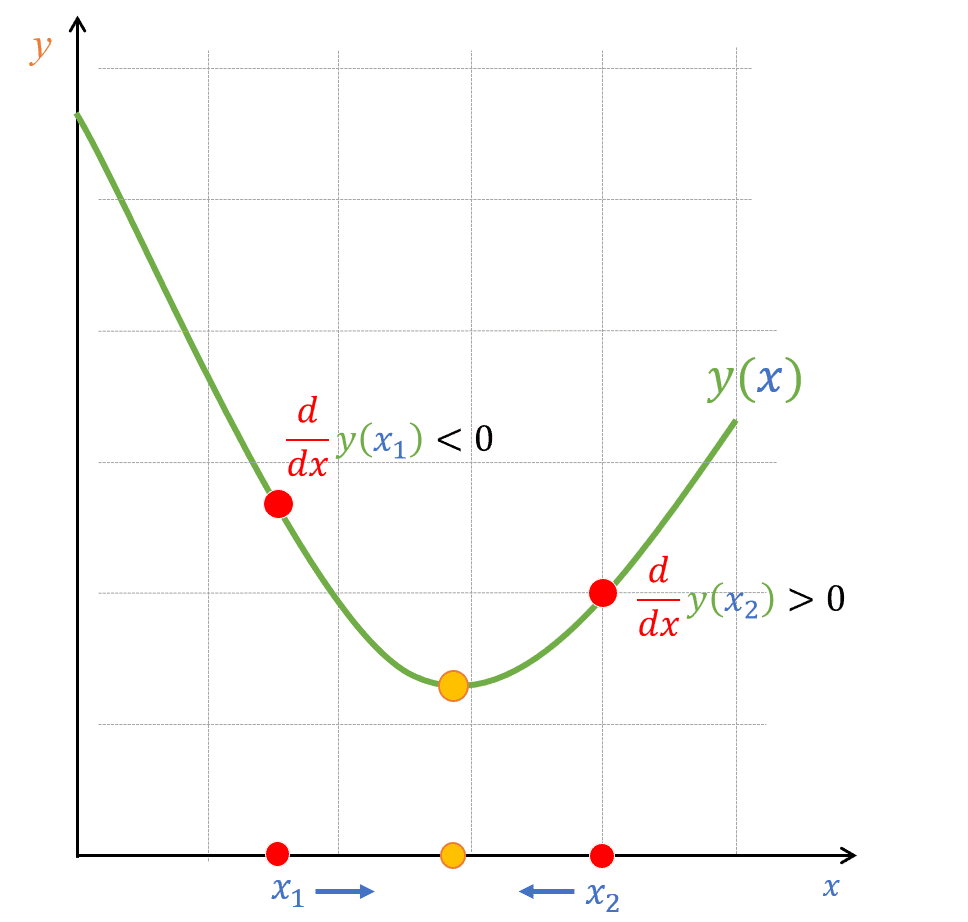 Hình 12: Giá trị đạo hàm (độ dốc) tại các điểm khác nhau.
Hình 12: Giá trị đạo hàm (độ dốc) tại các điểm khác nhau.
Nếu giá trị đạo hàm dương, ta biết rằng hàm số đang tăng tại điểm đó. Ngược lại, nếu giá trị đạo hàm âm, ta biết rằng hàm số đang giảm tại điểm đó (như Hình 12). Tận dụng tính chất này, chúng ta có thể dùng thông tin đạo hàm để giúp đẩy điểm đang ở một vị trí bất kỳ tiến về điểm cực tiểu bằng cách đi ngược về hướng đạo hàm:
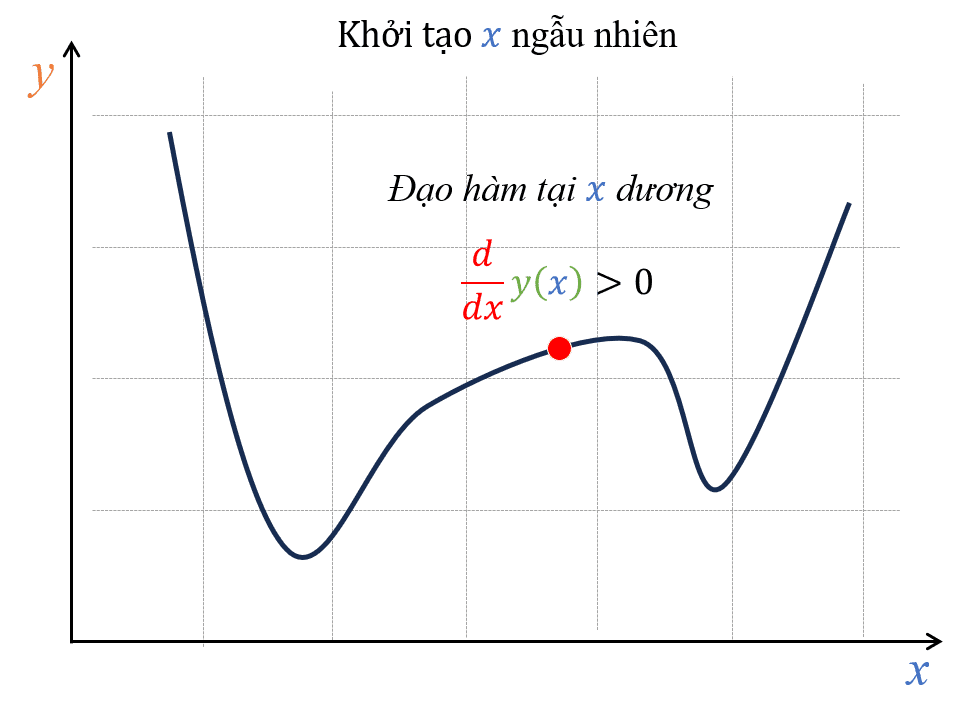 Hình 13: Khởi tạo một x bất kỳ và tính đạo hàm tại điểm đó.
Hình 13: Khởi tạo một x bất kỳ và tính đạo hàm tại điểm đó.
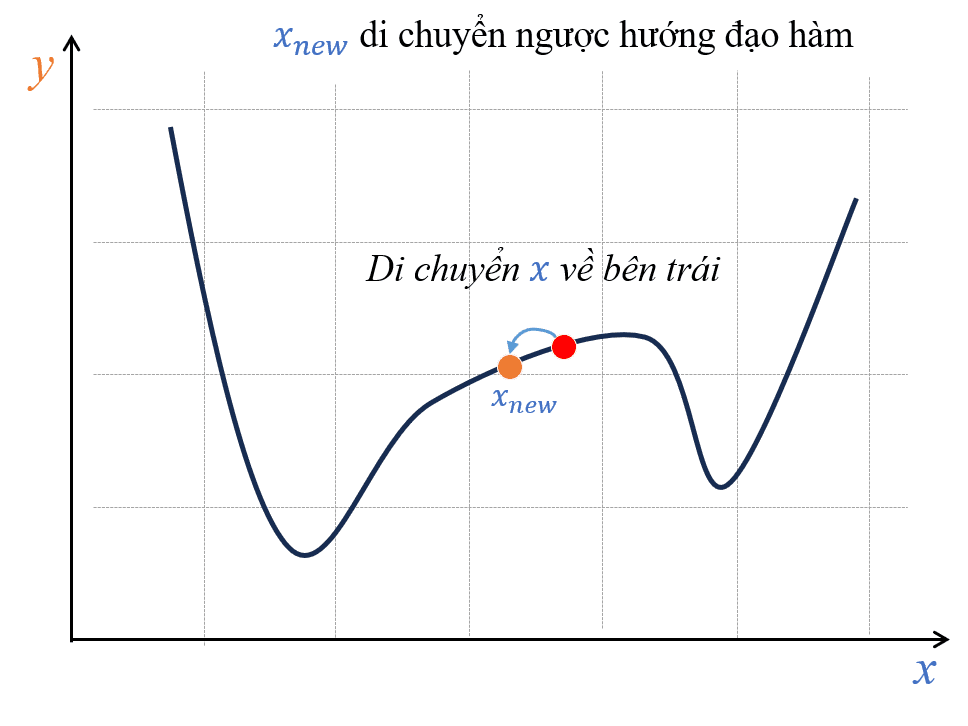 Hình 14: Áp dụng tính chất đi ngược hướng đạo hàm để tiến về cực tiểu.
Hình 14: Áp dụng tính chất đi ngược hướng đạo hàm để tiến về cực tiểu.
Hãy thử lấy ví dụ một hàm bất kỳ có hình dạng như Hình 13, nếu ta khởi tạo một điểm x bất kỳ và có đạo hàm tại điểm x này lớn hơn 0 (hoặc có thể quan sát thấy hàm đang tăng thì nghĩa là đạo hàm đang dương). Để tìm được điểm cực tiểu, ta sẽ đi ngược hướng đạo hàm, đó là đi sang trái (xem Hình 14).
Và nếu hành động này cứ được tiếp diễn, dần dần ta sẽ có thể đưa được điểm tiến gần đến điểm cực tiểu như hình sau:
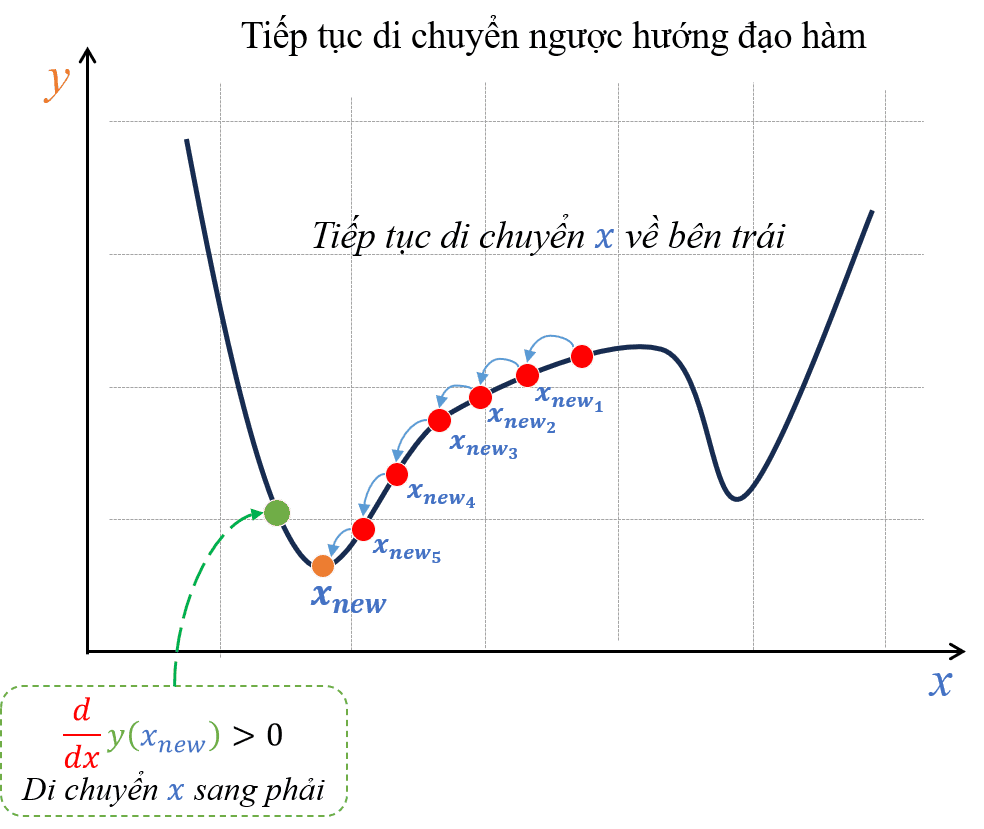 Hình 15: Lặp lại quá trình tính đạo hàm và di chuyển ngược hướng đạo hàm cho đến khi điểm x làm cho hàm y đạt giá trị cực tiểu.
Hình 15: Lặp lại quá trình tính đạo hàm và di chuyển ngược hướng đạo hàm cho đến khi điểm x làm cho hàm y đạt giá trị cực tiểu.
Từ đây, ý tưởng từ đây được hình thành như sau: Với lần lượt các điểm dữ liệu có sẵn, ta thực hiện tính đạo hàm tại điểm đang xét và cập nhật lại giá trị nhằm đưa tiến gần đến điểm cực tiểu của hàm loss, dẫn đến ta có một đường thẳng tối ưu cho bài toán dự đoán tiền lương. Tổng hợp lại toàn bộ các thông tin trên, ta sẽ có một quy trình các bước tính toán (pipeline) để tìm được đường thẳng tối ưu như sau:
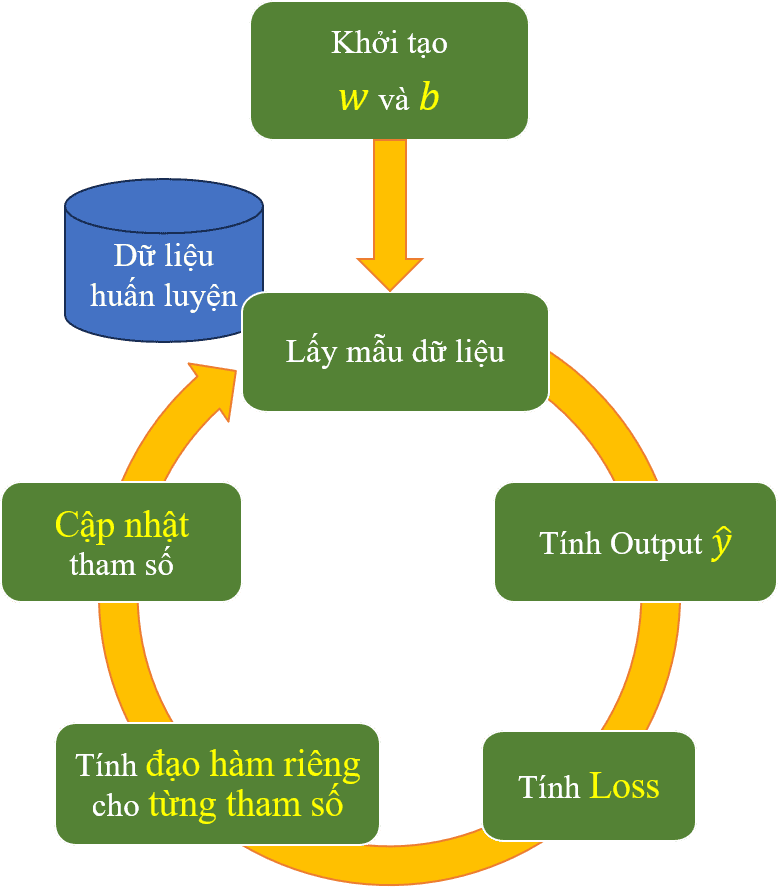 Hình 16: Pipeline tổng quan các bước tính toán để tìm tham số w và b tối ưu.
Hình 16: Pipeline tổng quan các bước tính toán để tìm tham số w và b tối ưu.
Vì đường thẳng được xác định từ hai biến là và , ta xét trường hợp tổng quát trong pipeline này bao gồm đi tìm giá trị tối ưu cho hai biến và . Như vậy, các bước thực hiện trong pipeline trên có thể diễn giải như sau:
Sau đó, như đã đề cập, ta lặp lại quy trình ở bước 2 cho đến khi xử lý hết tất cả các mẫu dữ liệu trong bộ dữ liệu.
Dựa theo cách triển khai đã đề cập ở phía trên, chúng ta sẽ thử áp dụng để xây dựng một hàm có khả năng dự đoán số tiền lương của nhân viên dựa theo số năm kinh nghiệm của họ. Đầu tiên, chúng ta xem qua một bộ dữ liệu nhỏ theo bảng dưới đây:
| Index | Experience | Salary (.million VND) |
|---|---|---|
| 0 | 3 | 60 |
| 1 | 4 | 55 |
| 2 | 5 | 66 |
| 3 | 6 | 93 |
Bộ dữ liệu trên gồm có 4 mẫu (sample), ứng với số năm kinh nghiệm (Experience) sẽ có số tiền lương tương ứng (Salary). Ví dụ, tại mẫu dữ liệu có Index bằng 1, một nhân viên có 4 năm kinh nghiệm sẽ có tiền lương tương ứng là 55 triệu VND. Với đề bài trên, ta sẽ tiến hành áp dụng thuật toán mô tả ở phần Dẫn nhập theo từng bước như sau:
Khởi tạo giá trị ngẫu nhiên cho hai tham số và . Ở đây, mình giả sử và . Chúng ta cũng sẽ chọn giá trị để sử dụng cho phần cập nhật tham số.
Với hai giá trị này, ta thử áp dụng các công thức dự đoán và tính loss để dùng cho việc so sánh giữa giá trị trước và sau khi áp dụng thuật toán xem mức độ hiệu quả đến đâu. Đầu tiên, ta sẽ dự đoán mức lương của một nhân viên có 7 năm kinh nghiệm với công thức sau:
Tiếp theo là tính loss, mình sẽ dự đoán dựa trên trực giác dựa theo dữ liệu có được, nhìn chung số năm kinh nghiệm càng lớn thì mức lương càng cao. Mình nghĩ mức lương cho một nhân viên 7 năm sẽ là 100 triệu. Vậy loss sẽ có giá trị bằng:
Như có thể thấy, với giá trị loss tương đối cao, do đó, kết quả dự đoán của mô hình không được như mong đợi. Để cải thiện mô hình Linear Regression, chúng ta sẽ từng bước điều chỉnh các tham số w và b sao cho phù hợp với bộ dữ liệu trên.
Ta tiến hành duyệt qua lần lượt các mẫu trong bộ dữ liệu: Trước tiên là mẫu dữ liệu thứ 0, gồm có , và thực hiện các bước tính toán:
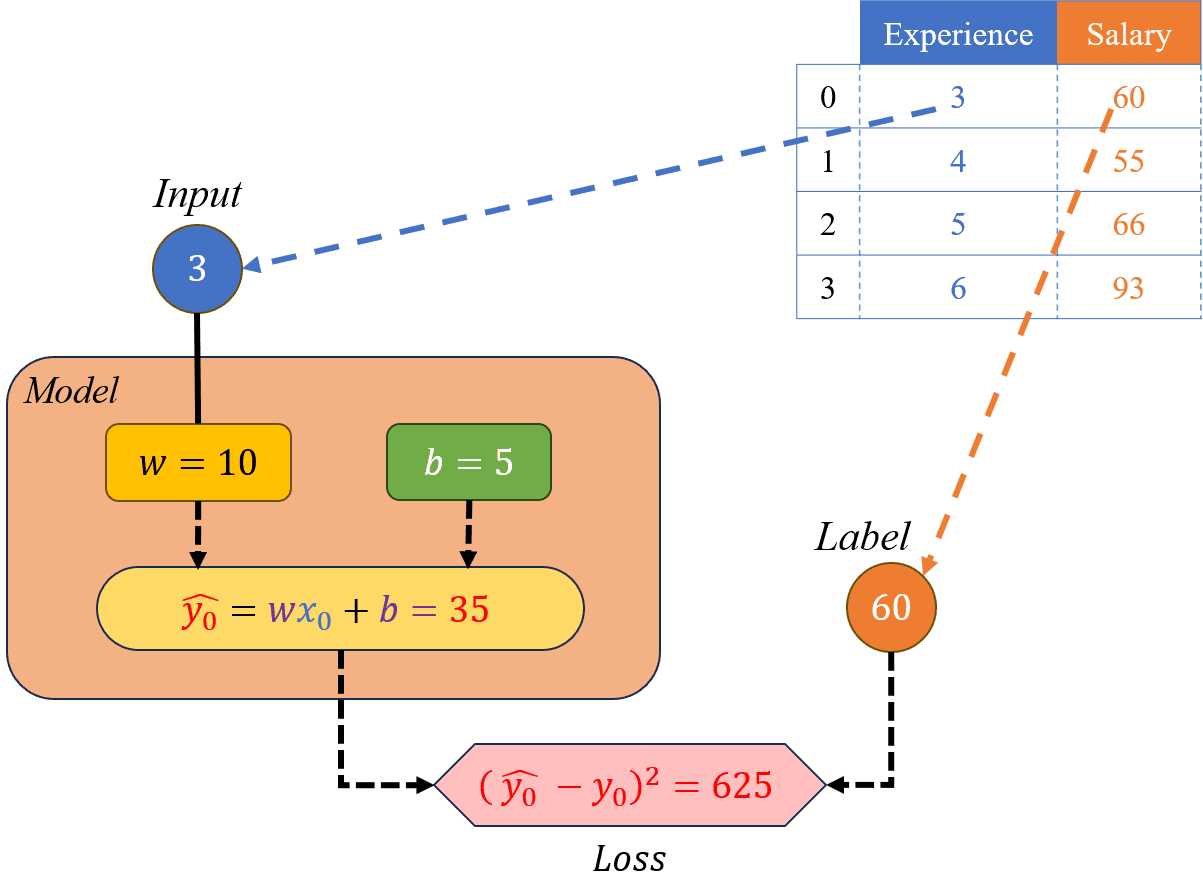 Hình 17: Minh hoạ cho các bước 2.1 và 2.2.
Hình 17: Minh hoạ cho các bước 2.1 và 2.2.
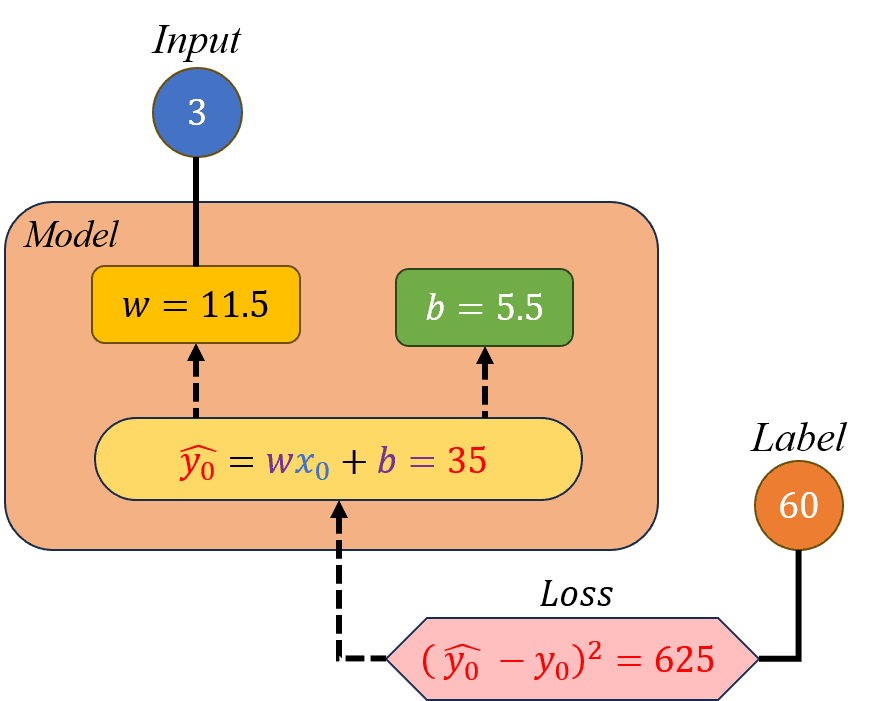 Hình 18: Minh hoạ cho các bước 2.3 và 2.4.
Hình 18: Minh hoạ cho các bước 2.3 và 2.4.
Lặp lại như bước (2) cho mẫu dữ liệu tiếp theo gồm có , và thực hiện các bước tính toán:
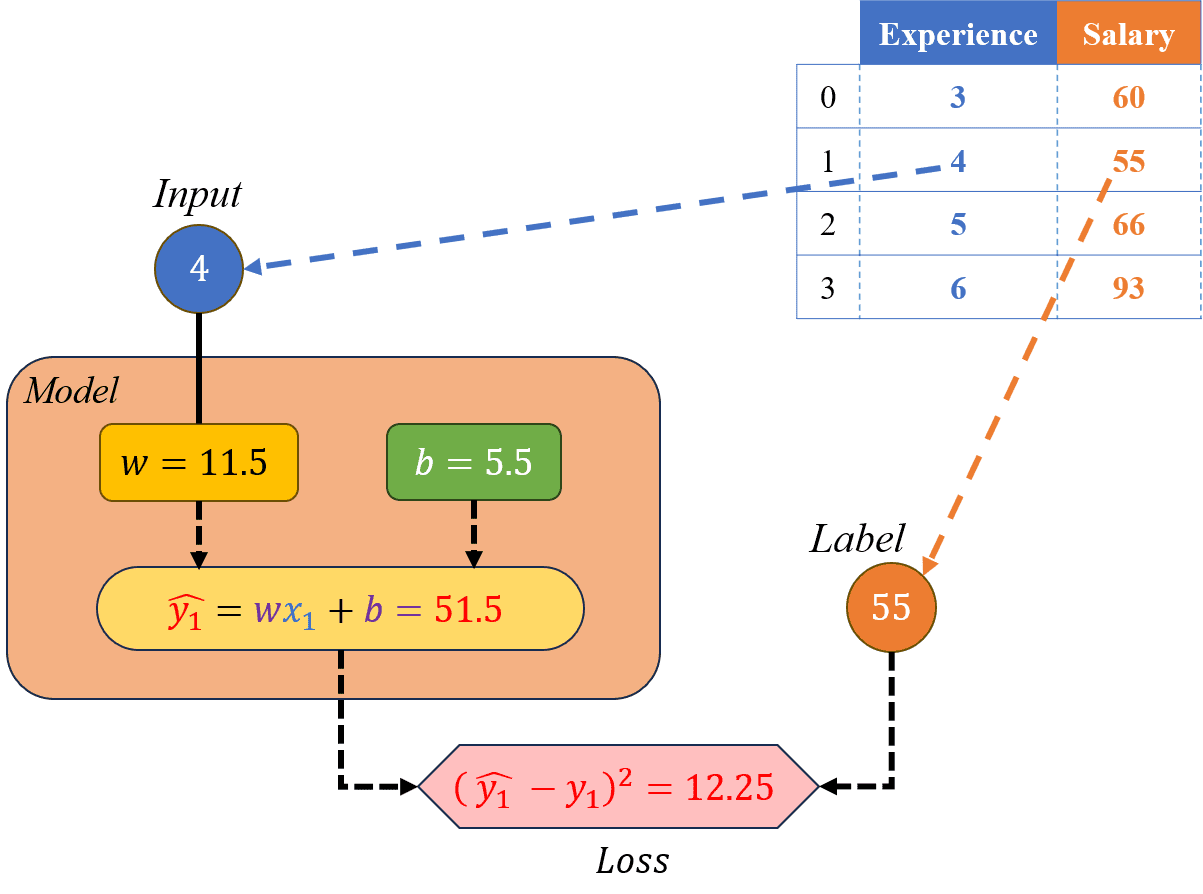 Hình 19: Minh hoạ cho các bước 3.1 và 3.2.
Hình 19: Minh hoạ cho các bước 3.1 và 3.2.
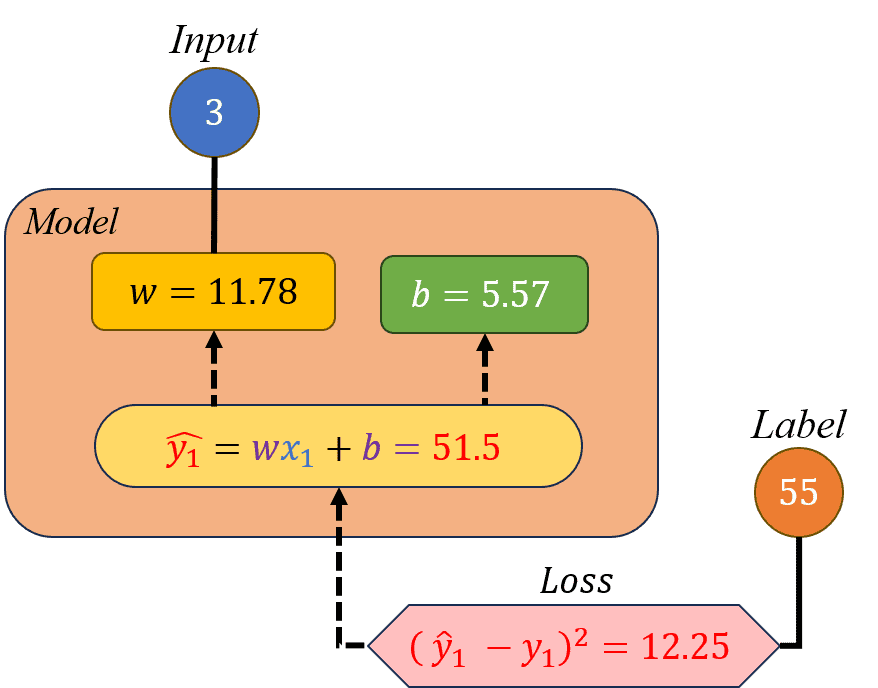 Hình 20: Minh hoạ cho các bước 3.3 và 3.4.
Hình 20: Minh hoạ cho các bước 3.3 và 3.4.
Thực hiện tương tự như đã làm với mẫu dữ liệu 0 và 1, ta lấy mẫu dữ liệu gồm có , và thực hiện các bước tính toán:
Với mẫu dữ liệu cuối cùng gồm có , và thực hiện các bước tính toán tương tự:
Sau khi duyệt qua tất cả các mẫu dữ liệu và các tham số w và b cũng đã được điều chỉnh lại cho phù hợp hơn với bộ dữ liệu của chúng ta. Để kiểm chứng điều này, ta sẽ thử dự đoán mức lương và tính loss với giá trị w và b mới này cho nhân viên có 7 năm kinh nghiệm. Trước tiên, mức lương của người nhân viên này là:
Kết quả dự đoán có vẻ tốt hơn ban đầu và đúng với mong đợi hơn. Để chắc chắn hơn, sau đây là giá trị loss với dự đoán này:
Với kết quả loss nhỏ hơn so với ban đầu (7.3984 < 625) cho thấy mô hình đã được học và điều chỉnh lại các tham số bên trong sao cho phù hợp hơn với dữ liệu huấn luyện và có thể được sử dụng để dự đoán các dữ liệu mới từ bên ngoài mà vẫn đảm bảo độ chính xác cao.
Tóm lại, Simple Linear Regression được khởi tạo với các tham số và có giá trị ngẫu nhiên, các tham số này sau đó sẽ được điều chỉnh lại dựa trên dữ liệu được học, sao cho tối ưu nhất có thể. Dẫu vậy, đây cũng chỉ là một phiên bản đơn giản, trong các bài học tiếp theo, chúng ta sẽ đi sâu hơn vào từng bước "học" của mô hình và khái quát hơn cho các trường hợp tổng quát.
- Hết -
Bài viết liên quan
Giải thuật di truyền (Genetic algorithm)
tháng 5 2025
Tài liệu này minh họa chi tiết từng bước hoạt động của giải thuật di truyền, một phương pháp tối ưu hóa được dùng phổ biến trong rất nhiều lĩnh vực khác nhau.